Introduction#

Objectif#

Dans ce cours, nous allons nous focaliser sur le contrôle et la commande des systèmes à une entrée / une sortie (SISO: Single Input Single Output). Un système SISO peut être représenté un bloc prenant une entrée et renvoyant une sortie.

En asservissement, notre objectif est de venir élaborer, synthétiser un signal de commande analogique ou numérique du processus que nous souhaitons contrôler. Pour atteindre cet objectif, nous proposons :

de mesurer la sortie du système au moyen d’un capteur,
de mesurer la différence entre la consigne et la sortie du capteur au moyen d’un comparateur,
d’élaborer un signal de commande à partir de la sortie du comparateur.

Cette structure correspond à un système bouclé puisque la sortie est combinée avec l’entrée via le comparateur.

Pour faciliter l’analyse des systèmes bouclés, nous travaillerons le plus souvent avec des systèmes bouclés à retour unitaire. En notant \(e(t)\) et \(s(t)\) le signal de consigne et le signal en sortie de capteur, nous obtenons alors le schéma bloc suivant.

Critères de Performance#

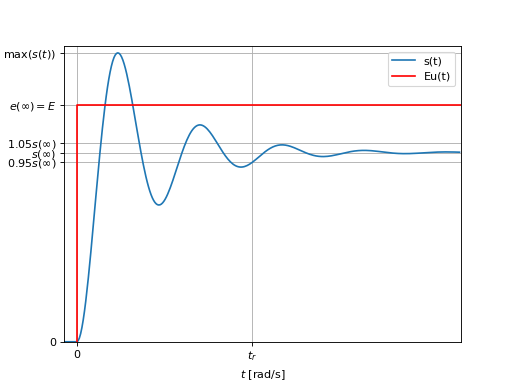
Pour élaborer un signal de commande, nous allons prendre en compte plusieurs contraintes portant sur l’allure du signal de sortie \(s(t)\). A titre d’illustration, la courbe suivante présente l’allure de la réponse d’un système à une entrée de type échelon (réponse indicielle). A partir de cette réponse, nous pouvons évaluer plusieurs critères permettant de critiquer les performances de l’asservissement.

Stabilité#

La première chose à évaluer est la stabilité du système. Un système est dit stable, au sens BIBO (Bounded Input Bounded Output), si et seulement si pour tout \(t\)

\[|e(t)|<\infty ~\Rightarrow~|s(t)|<\infty\]

En d’autres termes, une entrée bornée doit conduire à une sortie bornée.

Précision#

Une autre caractéristique importante d’un asservissement est sa précision. Pour mesurer la précision, un critère possible consiste à mesurer l’écart statique entre l’entrée et la sortie c-à-d \(\epsilon = e(\infty)-s(\infty)\). En pratique, nous préférons utiliser l’écart statique relatif qui est une mesure généralement indépendante de l’amplitude de l’entrée.

L’écart statique relatif est défini par :

\[\epsilon_r (\%) = 100 \times \left(\frac{e(\infty)-s(\infty)}{e(\infty)}\right)\]

Pour un système précis, l’écart statique relatif doit être nul.

Rapidité#

En plus du comportement statique, il est souvent important de critiquer le comportement dynamique du système. Pour critiquer le comportement dynamique, il est courant d’analyser la rapidité du système via sa réponse indicielle. Pour mesurer la rapidité, un critère possible est le temps de réponse à \(\pm 5\%\).

Le temps de réponse à \(\pm 5\%\) est défini par :

\[\forall t>t_r,~0.95 s(\infty) \le s(t) \le 1.05 s(\infty)\]

En d’autres termes, le temps de réponse correspond au temps nécessaire pour rentrer définitivement dans une fourchette comprise entre \(-5\%\) et \(+5\%\) de la valeur finale. Plus un système est rapide, plus son temps de réponse est faible.

Dépassement#

Une autre caractéristique importante concerne la présence ou nom d’oscillation au niveau de la réponse indicielle. Pour quantifier les oscillations, une critère possible consiste à mesurer le premier dépassement \(D = \max[s(t)]-s(\infty)\). Le plus souvent, nous préférons utiliser la valeur du premier dépassement relatif qui est une mesure généralement indépendante de la valeur finale.

Le premier dépassement relatif est défini par

\[D_r(\%)=100 \times \frac{\max[s(t)]-s(\infty)}{s(\infty)}\]

Robustesse#

Le plus souvent, l’analyse d’un système est réalisé sous l’hypothèse que nous connaissons exactement les comportements des différents blocs. Le plus souvent, ces comportements sont modélisés par des équations différentielles ou par des équations aux différences. Cette modélisation est, dans le meilleur des cas, une approximation de la réalité. Dans ce contexte, il est important d’évaluer la robustesse des stratégies de commande en présence d’écart de modélisation.

Pour mesure la robustesse d’un asservissement, une approche couramment utilisée consiste à analyser l’influence de perturbations extérieures sur le comportement du système. Ces perturbations peuvent être déterministes ou aléatoires.