Diagrammes de Black Nichols

Introduction

Considérons un système LTI de fonction de transfert \(F(p)\).

La calibration des correcteurs en boucle fermée est très souvent réalisée à partir du domaine fréquentiel. Le domaine fréquentiel s’obtient en évaluant \(F(j\omega)\). La grandeur obtenue est généralement complexe. Pour la représenter, deux diagrammes sont couramment utilisés.

• Diagramme de Bode: représentation du module (en dB) en fonction de la pulsation, représentation de la phase (en deg) en fonction de la pulsation,

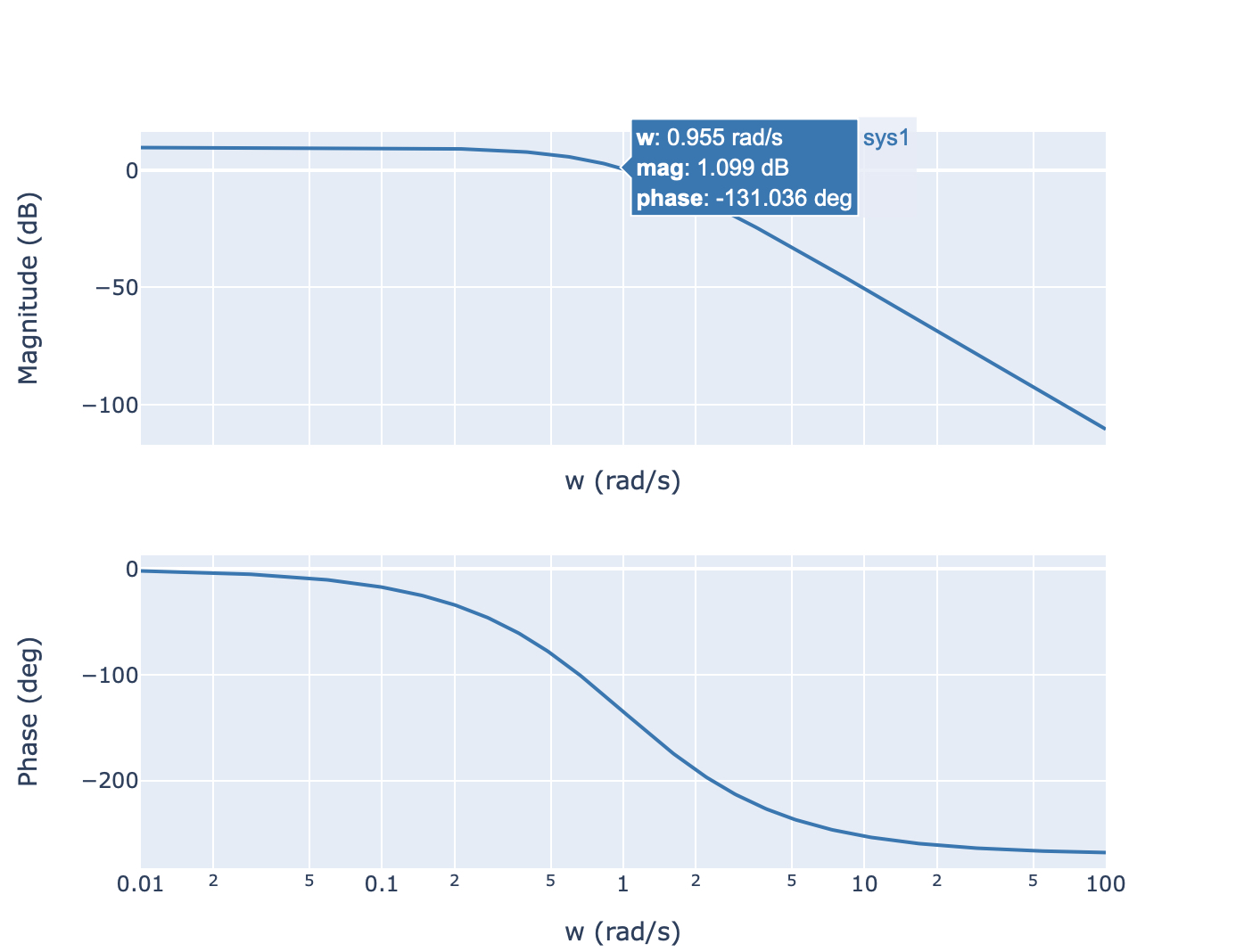
Diagramme de Bode du système

• Diagramme de Black-Nichols: représentation du module (en dB) en fonction de la phase (en deg).

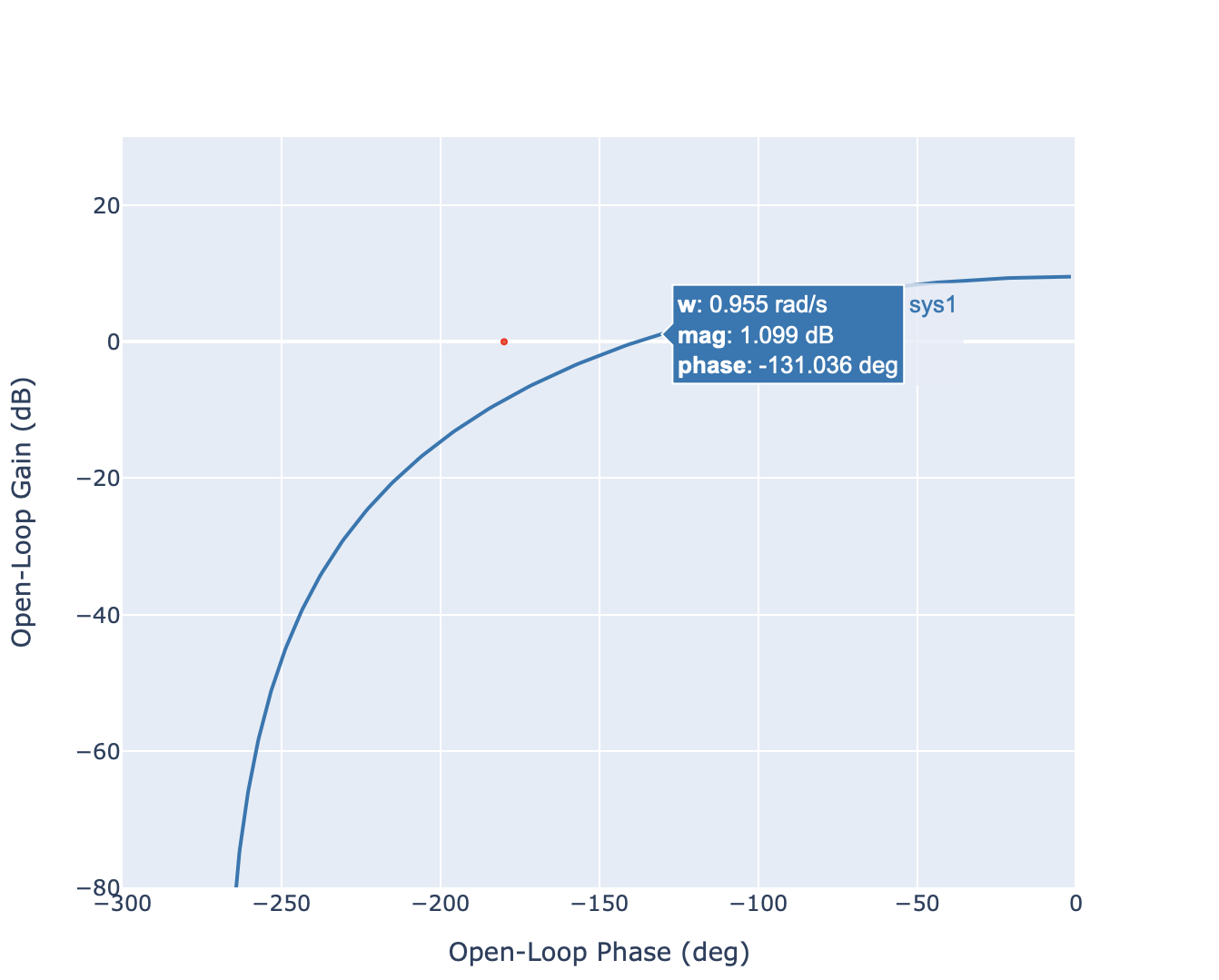
Diagramme de Black Nichols du système

Dans ce tutorial, nous montrons comment utiliser la représentation de Black-Nichols pour anticiper le comportement d’un système en boucle fermée avec un retour unitaire.

Principe

Considérons un système en boucle fermée avec un retour unitaire.

Le comportement de la boucle fermée peut être appréhendé à partir de diagramme de Black Nichols de la boucle ouverte en utilisant le point critique \((0dB,-180)\) et les contours d’iso-gain. Ces deux annotations sont utilisées de la manière suivante.

• Le point critique permet de conclure par rapport à la stabilité du système en boucle fermée.

• Les contours iso-gain permettent d’obtenir rapidement le gain en dB pour certaines pulsations en boucle fermée (avec retour unitaire). Ces informations sont ensuite utilisées pour appréhender le comportement dynamique de la boucle fermée.

Stabilité

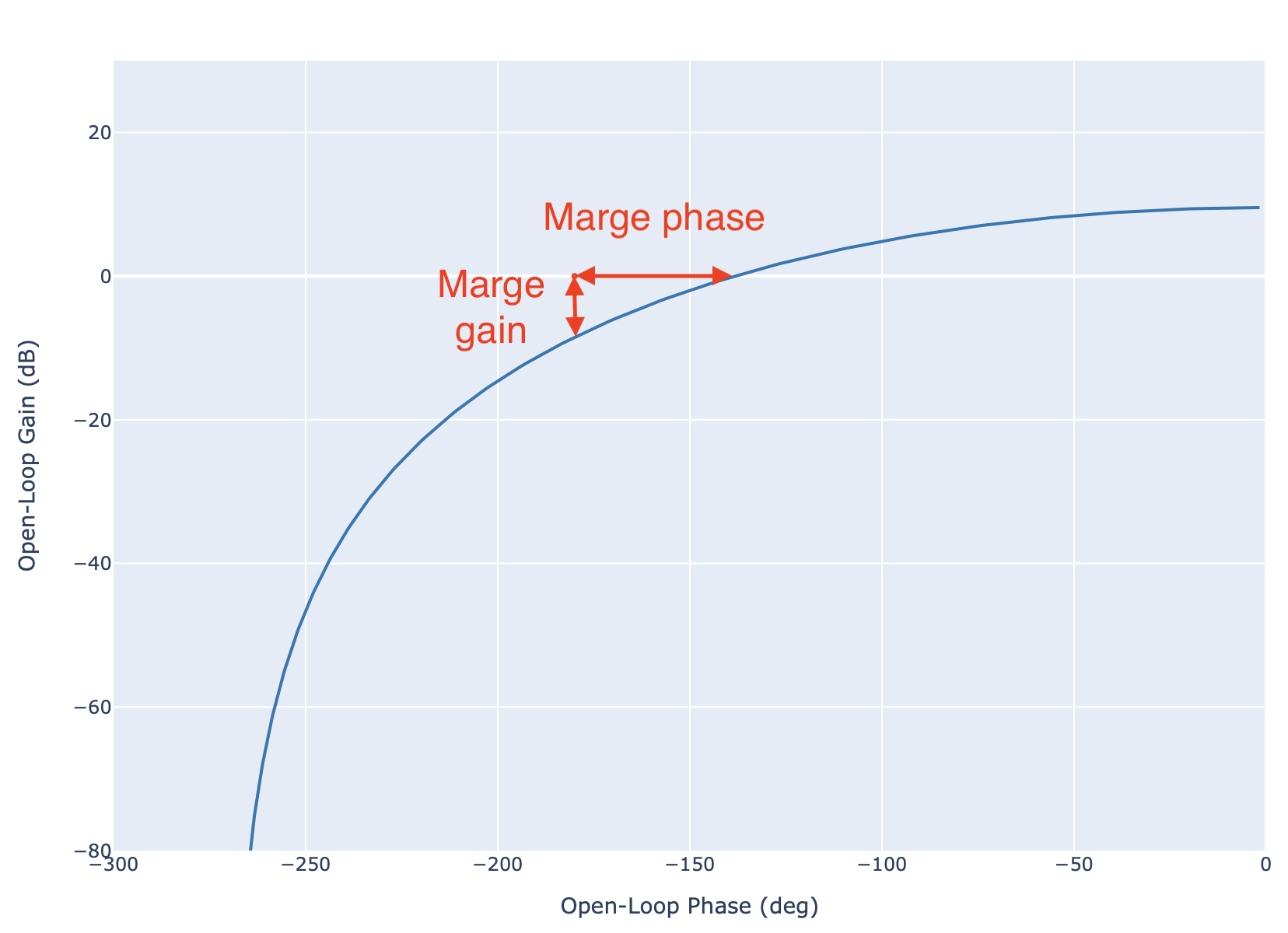
Diagramme de Black Nichols du système en boucle ouverte

Critère du revers

Le système en boucle fermée est stable si et seulement si, en parcourant le lieu de transfert de la boucle ouverte dans le sens des pulsations croissantes, le point critique \((0dB,-180)\) est laissé sur la droite.

A titre d’exemple, dans la figure précédente, nous pouvons remarquer que le critère du revers est bien vérifié car en parcourant le lieu de transfert dans le sens des \(\omega\) croissant (c-à-d de la droite vers la gauche), le lieu de transfert laisse le point critique sur sa droite. Le système sera stable en boucle fermée.

Le critère du revers est un critère binaire. En pratique, nous préférons utiliser les notions de

• marge de gain \(M_G\) (en dB),

• marge de phase \(M_{\varphi}\) (en degrés).

Ces deux marges indiquent la distance entre le lieu de transfert et le point critique.

Caractéristiques Fréquentielles

Les contours iso-gain permettent d’appréhender le comportement dynamique du système en boucle fermée. Pour remonter aux propriétés dynamiques, les contours sont utilisés pour extraire graphiquement le gain statique et la résonance du système \(M_{dB}\). Sous l’approximation que le système se comporte en boucle fermée comme un second ordre, il est ensuite possible de remonter jusqu’au coefficient d’amortissement \(m\) et à la pulsation propre \(\omega_n\).

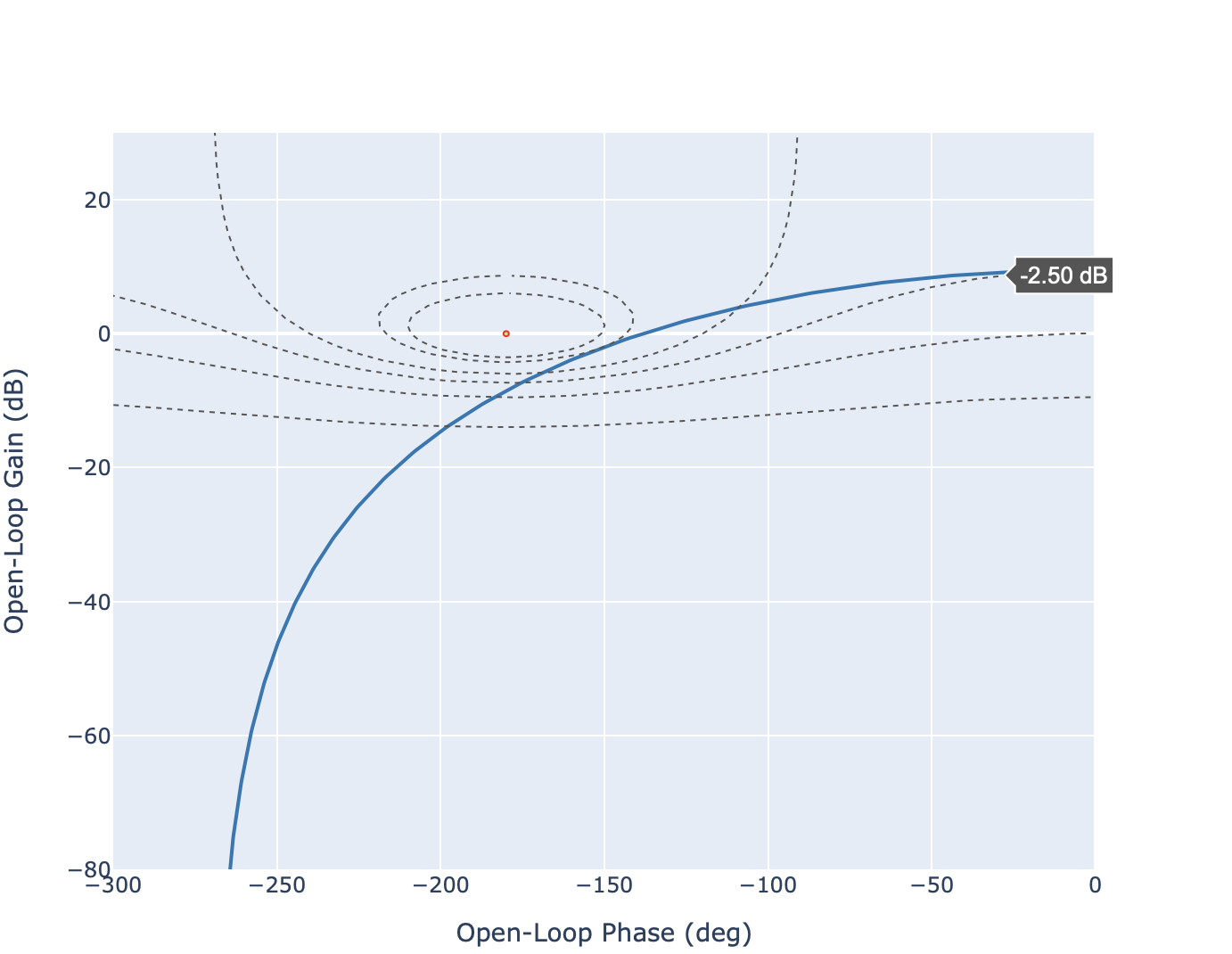
Diagramme de Black Nichols du système en boucle ouverte. Lecture du gain statique en dB.

• Gain statique en dB. Le gain statique en dB s’obtient en recherchant le contour iso-gain confondu avec le lieu de transfert en basse-fréquence. A partir de la courbe, nous trouvons:

\[G_0=-2.5~dB\]

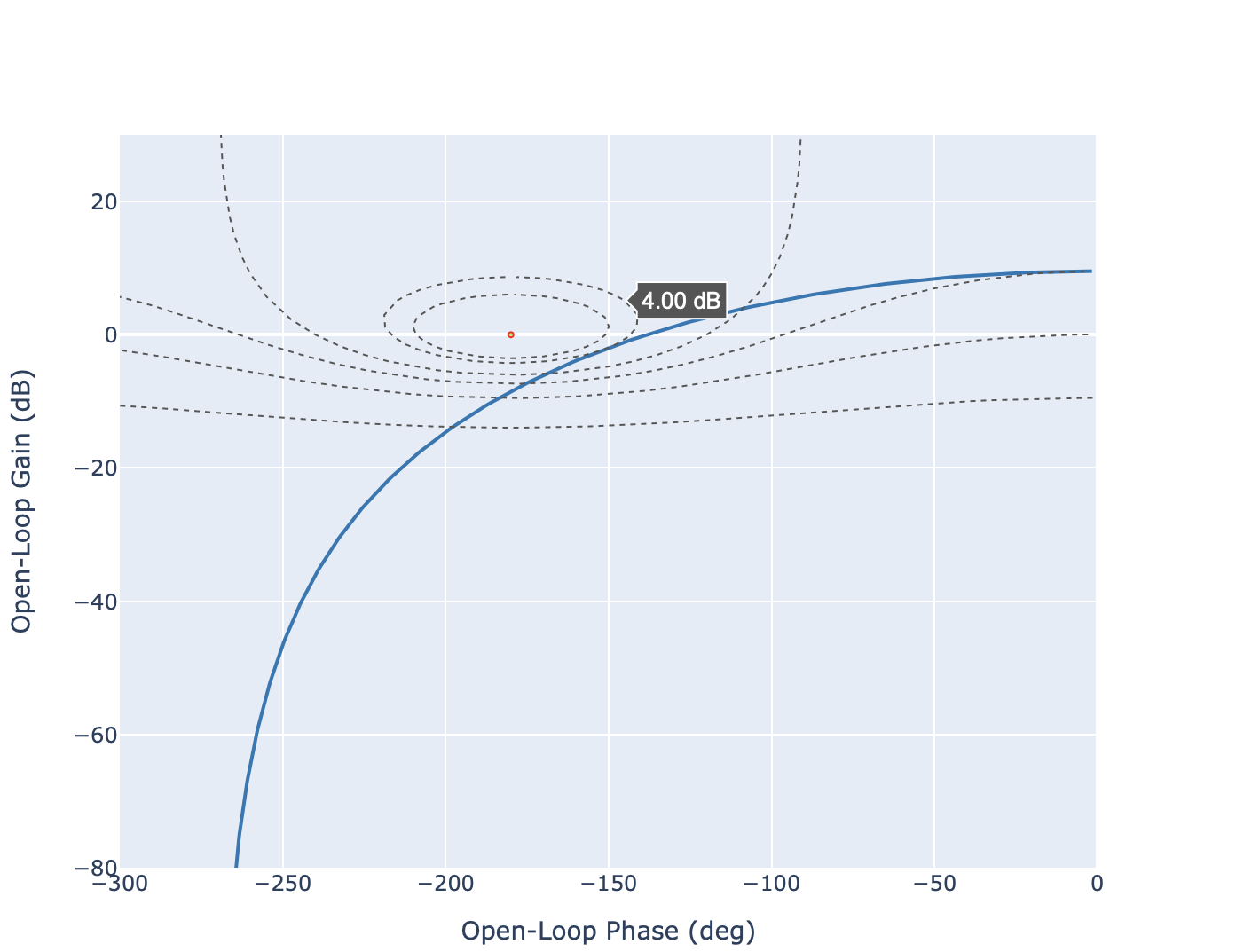
Diagramme de Black Nichols du système en boucle ouverte. Lecture du gain maximum en dB.

• Gain maximum en dB. Le gain maximum s’obtient en recherchant le contour iso-gain tangentant le lieu de transfert. A partir de la courbe, nous obtenons

\[G_m=4~dB.\]

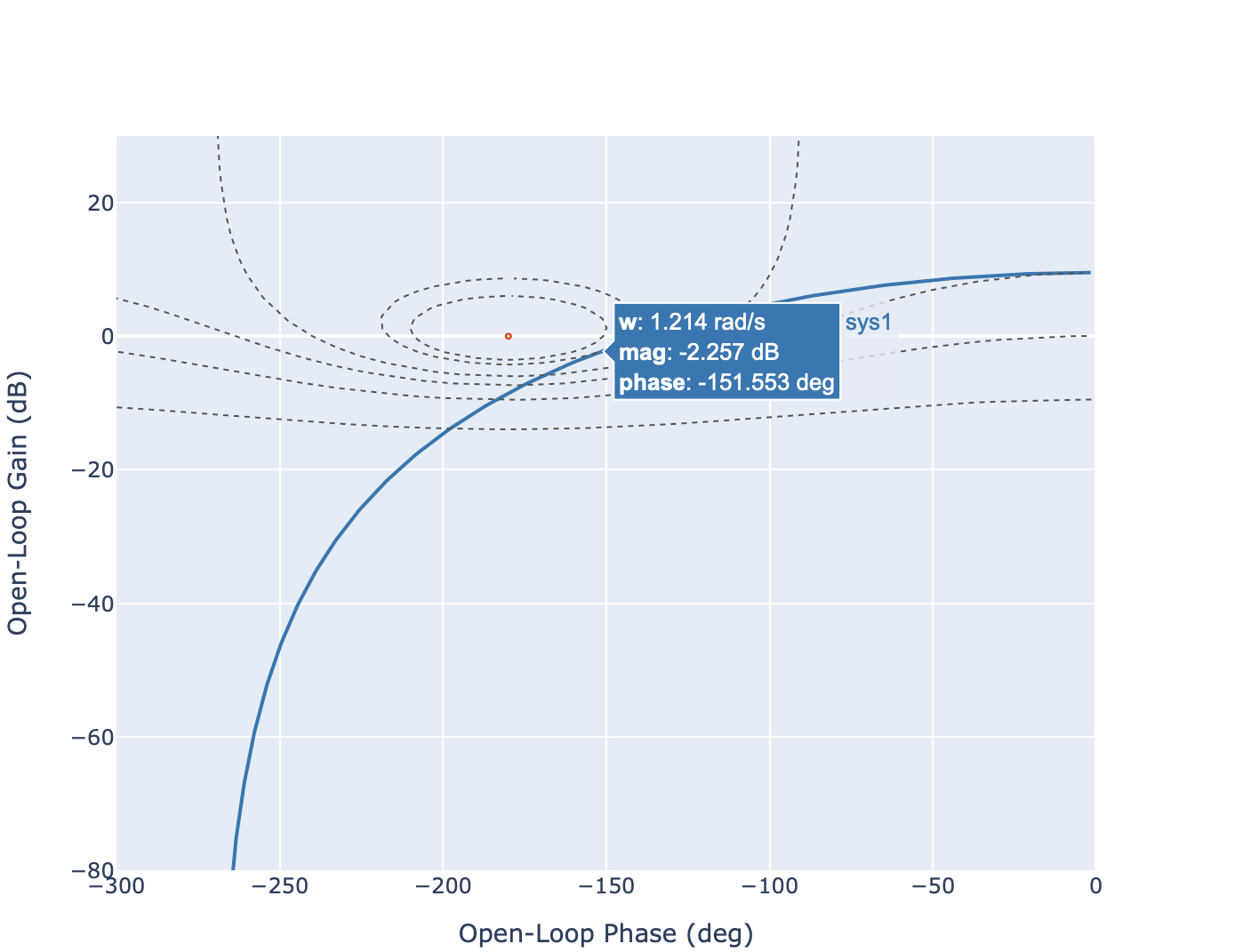
Diagramme de Black Nichols du système en boucle ouverte. Lecture de la pulsation de resonance.

• Pulsation de résonance. La pulsation de résonance (qui est différente de la pulsation propre) se lie directement à partir de la courbe au point de tangence. A partir de la courbe, nous obtenons

  \[\omega_r=1.214~rad/s\]

• Facteur de résonance en dB. Le facteur de résonance en dB s’obtient à partir de la différence entre le gain maximum en dB et le gain statique en dB. A partir de la courbe, nous obtenons

\[M_{dB} = G_m - G_0 = 6.5~dB.\]

Approximation Second Ordre

Il est possible d’appréhender le comportement en boucle fermée en considérant que le système se comporte en boucle fermée comme un système de second ordre:

\[H(p) \approx \frac{K}{\frac{1}{\omega_n^2}p^2+\frac{2m}{\omega_n}p+1}\]

Les paramètres du système s’obtiennent à partir des caractéristiques fréquentielles.

• Gain statique en valeur naturelle: \(K = 10^{G_0/20} \approx 0.75\)

• Coefficient d’amortissement: \(M_{dB}=6.5\) dB donc \(m\approx 0.24\) (voir abaques)

• Pulsation propre. Pour un système de second ordre, la pulsation de résonance s’exprime sous la forme \(\omega_r = \omega_n \sqrt{1-2m^2}\). En prenant \(m\approx 0.24\) et \(\omega_r=1.214\) rad/s, nous obtenons \(\omega_n \approx 1.290\) rad/s.

Caractéristiques Temporelles

En utilisant cette approximation second ordre, il est possible d’appréhender les caractéristiques temporelles de la réponse indicielle :

• Valeur finale: \(s(\infty)\approx 0.75E\) où \(E\) désigne l’amplitude de l’échelon.

• Premier dépassement relatif: \(m\approx 0.24\) donc \(D_r(\%)\approx 46\%\) (voir abaques)

• Temps de réponse à \(\pm 5\%\): \(m\approx 0.24\) donc \(\omega_n t_r = 10.83\) s (voir abaques). Il en vient que \(t_r \approx 8.39\) s

Verifications

Il est possible d’obtenir le comportement en boucle fermée en utilisant la fonction feedback de la librairie python-control. Les figures suivantes présentent la réponse indicielle du système en boucle fermée (échelon unitaire).

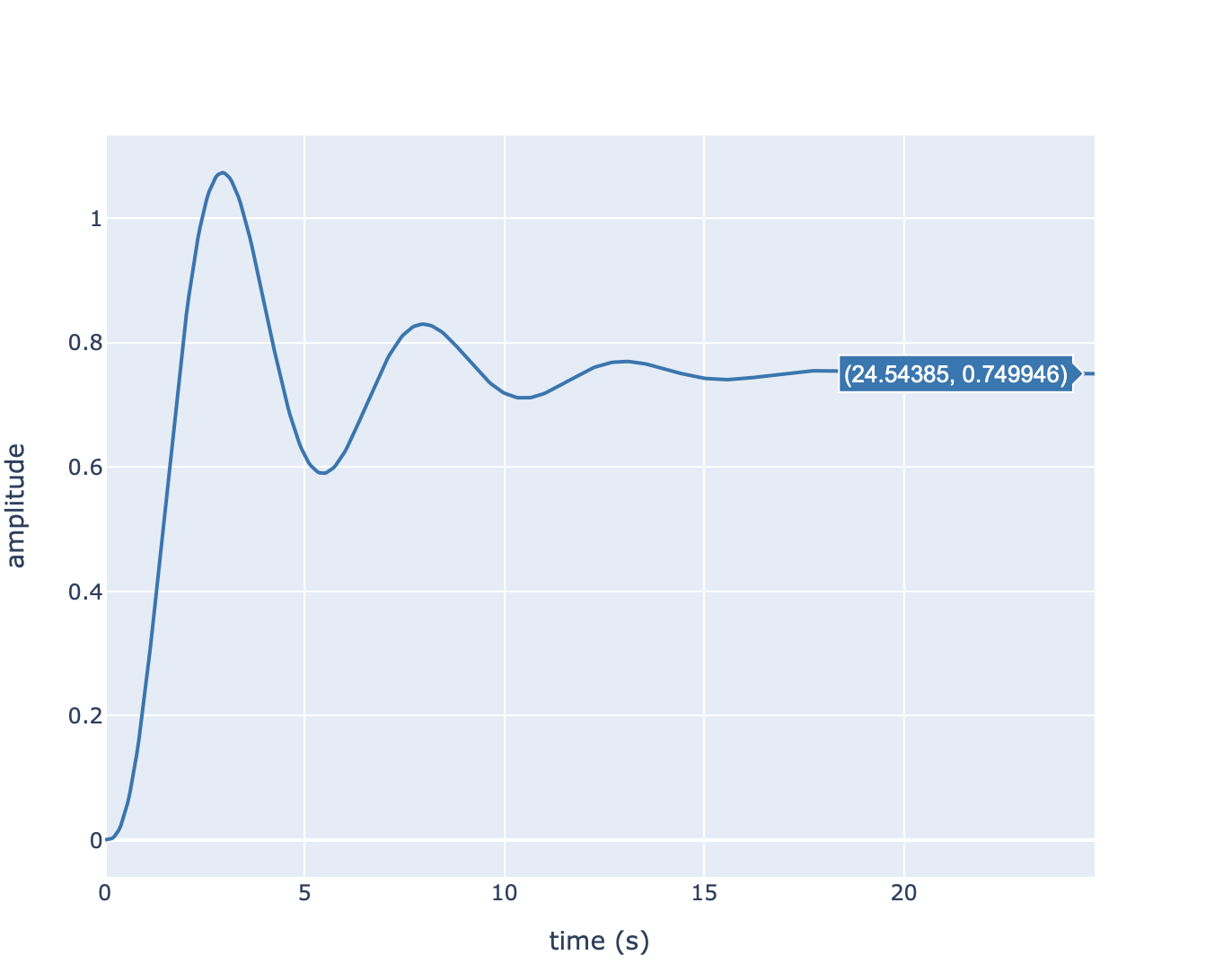
Réponse Indicielle de la boucle fermée.

• Valeur finale: \(s(\infty)= 0.75\)

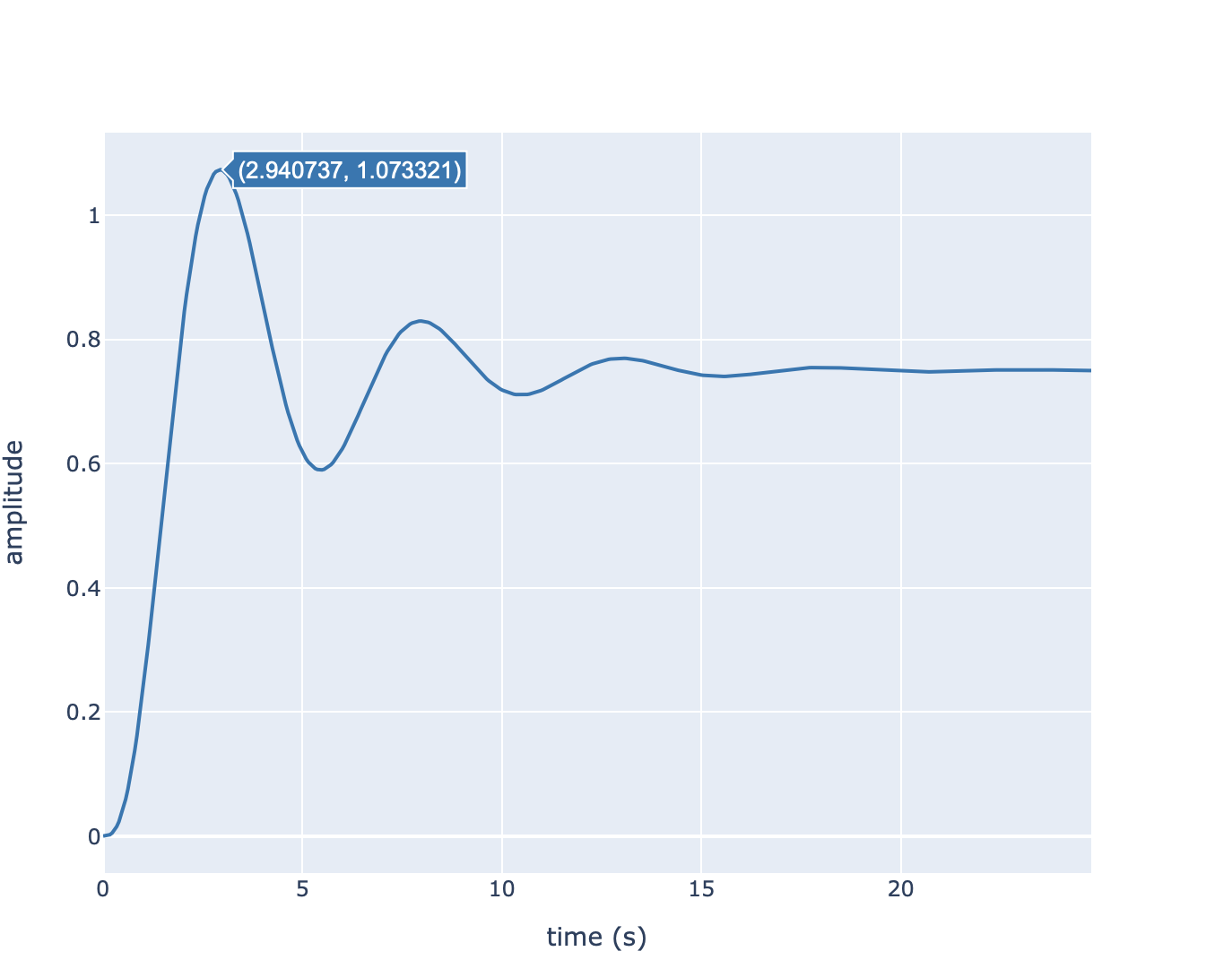
Réponse Indicielle de la boucle fermée

• Premier dépassement relatif:

\[D_r(\%) = \frac{\max(s(t))-s(\infty)}{s\infty}\times 100 \approx 43\%\]

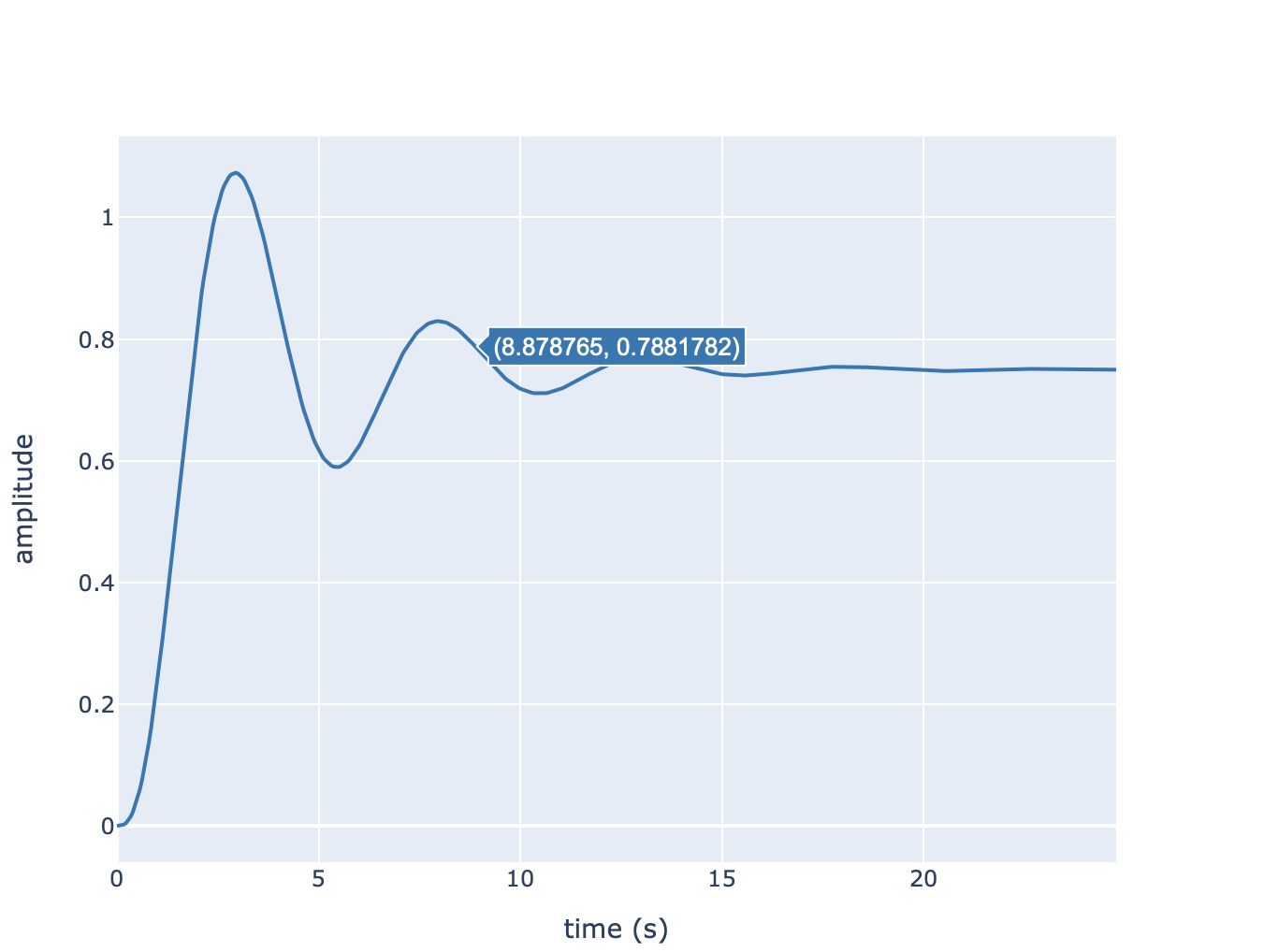
Réponse Indicielle de la boucle fermée

• Temps de réponse à \(\pm 5\%\): \(t_r \approx 8.87\) s