Correction P#
Contexte#
Dans ce tutorial, nous nous intéressons à la correction d’un système de 2ieme ordre avec un retour unitaire.
Dans ce tutorial, la fonction de transfert du système est égale à
Notre objectif est d’obtenir en boucle fermée un coefficient d’amortissement de \(m=0.52\).
Calibration#
Pour respecter ce cahier des charges, nous allons utiliser un correcteur proportionnel (P) :
Nous proposons de calibrer le paramètre du correcteur, \(K_i\), directement dans le plan de Black Nichols.
Black-Nichols#
Dans un premier temps, nous allons représenter le comportement fréquentiel du système \(F(p)\) en boucle ouverte.
from control import tf, feedback
from control_plotly import bode,nichols, step
F = tf([1],[1, 2, 1])
nichols(F, cm=[3, 0,-1.6, -2.6, -3, -6], show_phase=False)
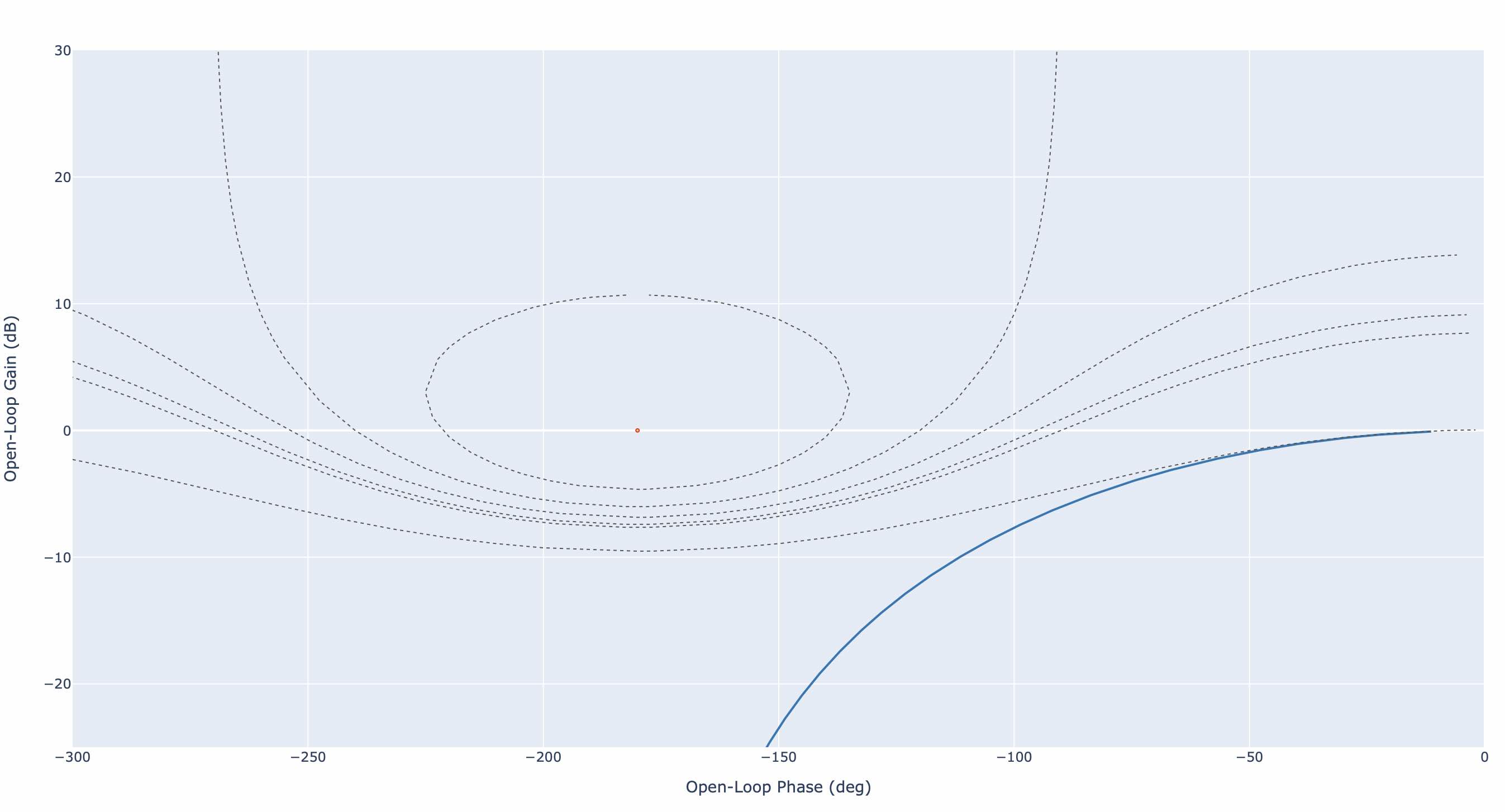
Diagramme de Black Nichols du système en boucle ouverte#
Choix du gain#
La seconde étape consiste à calibrer le gain proportionnel du correcteur. Pour calibrer ce gain, nous allons exploiter le comportement à la résonance. En approximant le comportement du système en boucle fermée par un second ordre, le facteur de résonance \(M_{dB}\) s’obtient à partir du coefficient d’amortissement \(m\) en utilisant les abaque de second ordre.
D’après les abaques, \(m=0.52\) correspond à un facteur de résonance de \(M_{dB}=G_m - G_0 = 1\) dB.
Après essais multiples, nous trouvons que le gain permettant d’obtenir la résonance souhaitée est égale à \(K_i=2.818\).
Ki = 2.8
nichols([F, Ki*F], cm=[3, 0,-1.6, -2.6, -3, -6],show_phase=False)
Les figures suivantes présentent le comportement fréquentiel du système original (bleu) et du système avec apport d’un gain \(K_i=2.818\) (orange). L’apport d’un gain supérieur à 1 a pour effet de translater le lieu de transfert vers le haut.
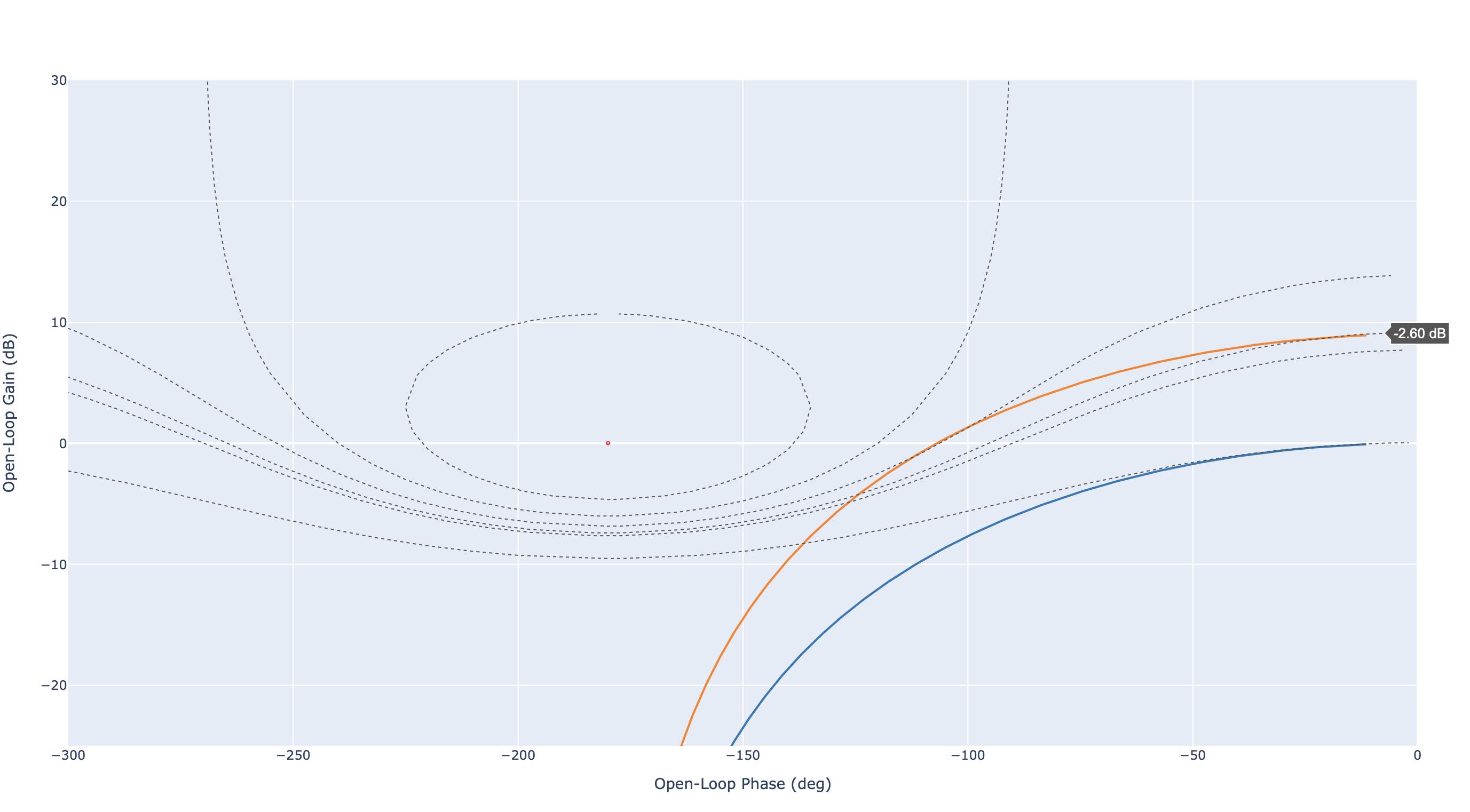
Diagramme de Black Nichols : correction proportionnelle (Gain statique \(G_0=-2.6\) dB)#
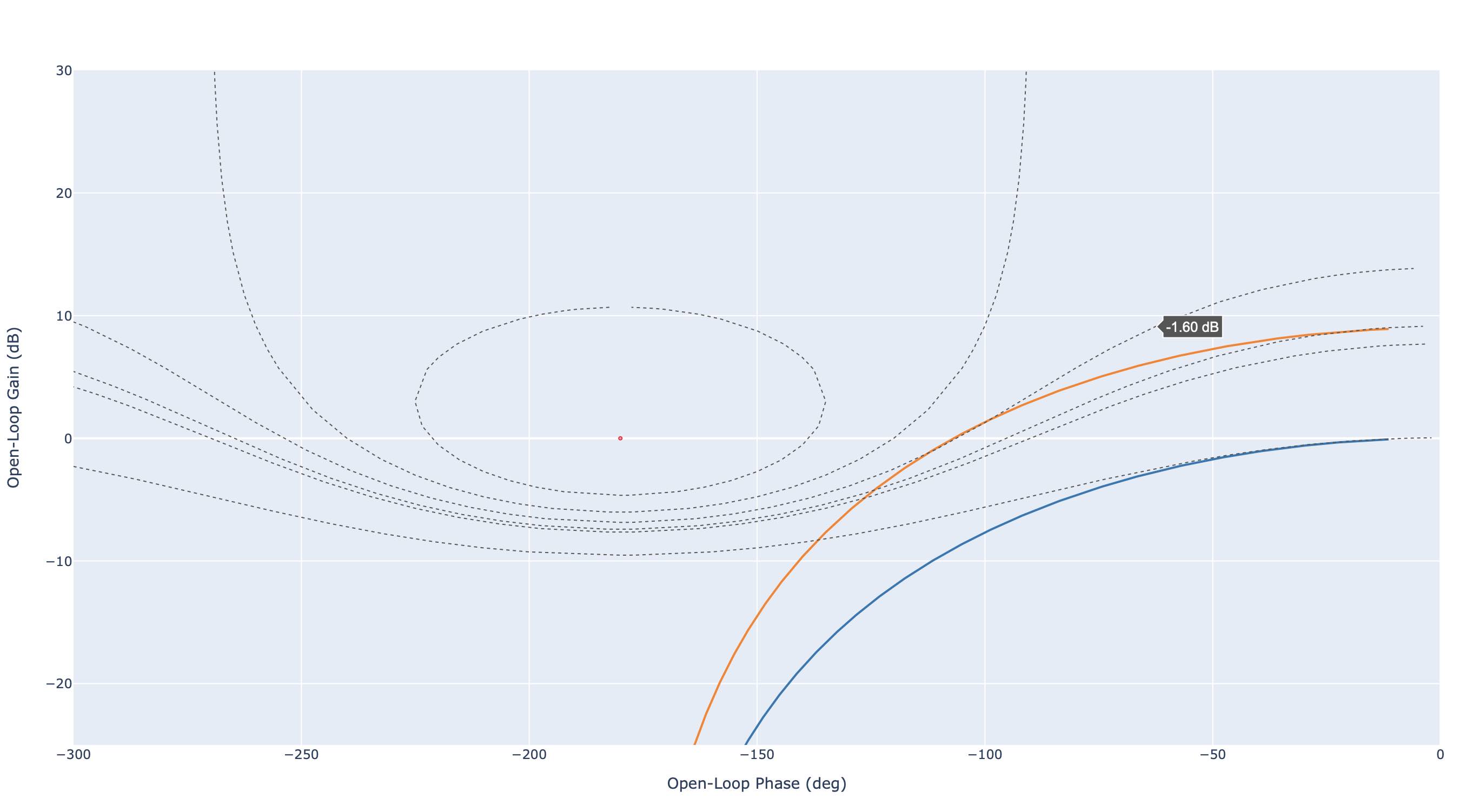
Diagramme de Black Nichols : correction proportionnelle (Gain maximum \(G_m=-1.6\) dB)#
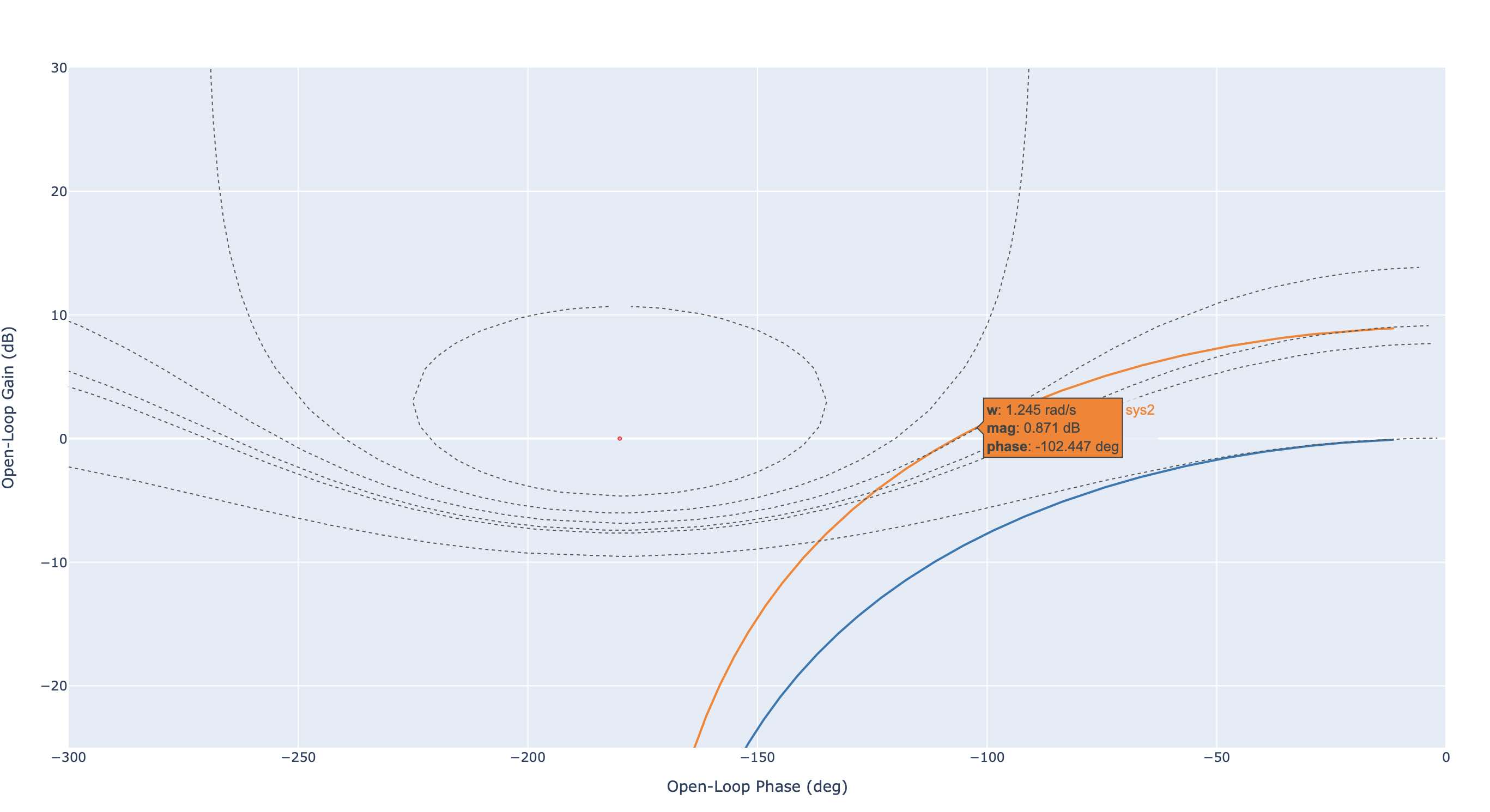
Diagramme de Black Nichols : correction proportionnelle (pulsation de résonance \(\omega_r =1.245\) rad/s)#
Notons qu’il est possible d’anticiper le comportement de la boucle fermée.
Gain statique: \(K=10^{G_0/20}=0.741\)
Premier dépassement relatif. En utilisant les abaques, nous trouvons \(14.77\%\)
Temps de réponse. Comme \(\omega_r = 1.245\) rad/s et \(m = 0.52\), il en vient que \(\omega_n = 1.837\) rad/s. En utilisant les abaques, nous trouvons que \(t_r\approx 2.8\) s.
Vérification#
La figure suivante présente la réponse indicielle du système en boucle fermée. Nous trouvons un premier dépassement relatif d’environ \(15\%\). Concernant la précision, nous remarquons que la valeur finale est égale à \(s(\infty) =0.74\) ce qui montre que le système est peu précis. Le temps de réponse mesuré est environ égal à \(t_r=2.72\) s.
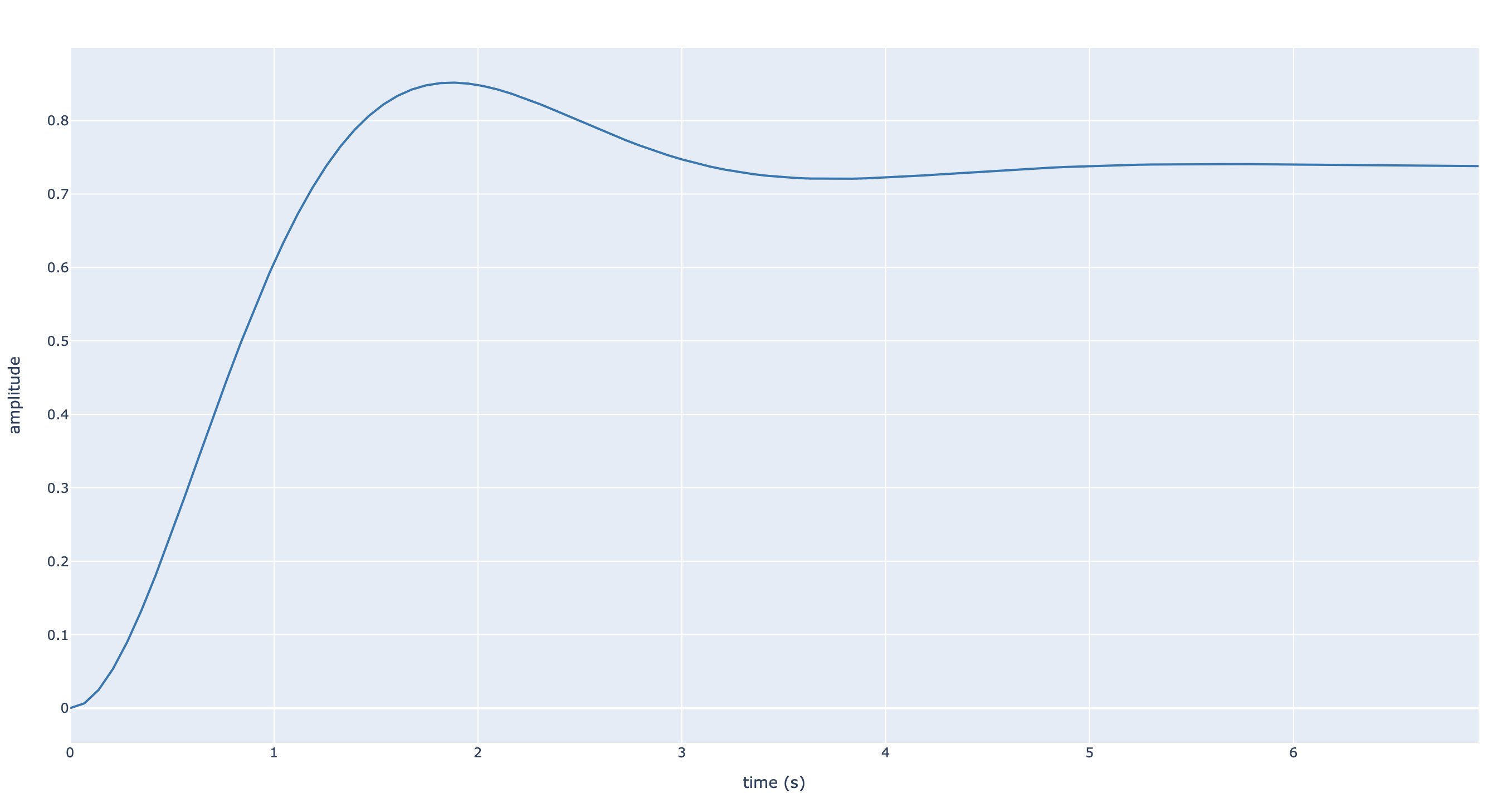
Réponse indicielle du système corrigé en boucle fermée (échelon unité)#