Systèmes de 2nd ordre#

Modélisation#

Equation Différentielle#

Pour un système passe-bas linéaire d’ordre 2, le lien entre l’entrée et la sortie peut être décrit par une équation différentielle de second ordre à coefficients constants.

\[\frac{1}{\omega_n^2}\frac{d^2 s(t)}{dt^2}+\frac{2m}{\omega_n}\frac{d s(t)}{dt}+s(t)=Ke(t)\]

  • \(K\) : gain statique,

  • \(m \ge 0\) : coefficient d’amortissement,

  • \(\omega_n\) : pulsation propre (en rad/s).

Notons que certains ouvrages préfèrent utiliser, au lieu du paramètre \(m\), le facteur de qualité

  • \(Q=\frac{1}{2m}\) : facteur de qualité.

Fonction de Transfert#

La fonction de transfert d’un système passe-bas de second ordre est donnée par :

\[H(p)=\frac{K}{\frac{1}{\omega_n^2}p^2+\frac{2m}{\omega_n}p+1}\]

Pôles#

Expression#

Les pôles correspondent aux valeurs de \(p\) pour lesquelles

\[\frac{1}{\omega_n^2}p^2+\frac{2m}{\omega_n}p+1 = 0\]

Le calcul des pôles s’obtient en recherchant les racines d’une équation du second degré. Le discriminant s’exprime sous la forme :

\[\Delta =\frac{4}{\omega_n^2}(m^2-1)\]

Nous pouvons alors distinguer trois cas de figure :

  • \(m>1\): deux pôles réels

    • \(p_{1}=-\omega_n(m-\sqrt{m^2-1})\)

    • \(p_{2}=-\omega_n(m+\sqrt{m^2-1})\)

  • \(m=1\): un pôle double

    • \(p_1 = p_2 = -m\omega_n\)

  • \(m<1\): deux pôles complexe-conjugués

    • \(p_{1}=-\omega_n(m-j\sqrt{1-m^2})\)

    • \(p_{2}=-\omega_n(m+j\sqrt{1-m^2})\)

Exemple#

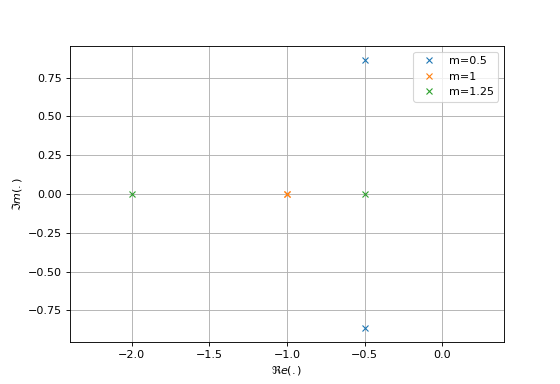
../../_images/second_order-1.png

Identification#

Lorsque \(0\le m<1\), l’identification de la pulsation propre et coefficient d’amortissement peut s’obtenir de la manière suivante:

  • Pulsation propre: la pulsation propre correspond au module des pôles c-à-d \(\omega_n=|p_{k}|\),

  • Coefficient d’amortissement: le coefficient d’amortissement s’obtient à partir de la partie réel des pôles via la relation \(m=-\Re e(p_{k})/|p_{k}|\).

Notons qu’il n’est pas possible d’identifier le gain statique en utilisant la position des pôles.

Réponse Indicielle#

Cas où \(m>1\)#

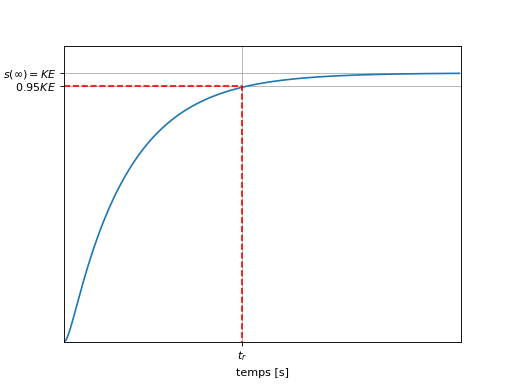
La figure suivante présente l’allure de la réponse indicielle lorsque \(m>1\). Dans ce contexte, la réponse est monotone et ne présente pas de dépassement.

../../_images/second_order-2.png

La réponse indicielle s’exprime sous la forme :

\[s(t)=KE\left(1-\frac{1}{2\omega_n\sqrt{m^2-1}}\left(p_1 e^{p_2 t}-p_2 e^{p_1 t} \right)\right)u(t)\]

Propriétés

  • Valeur initiale : \(s(0)=0\),

  • Valeur finale : \(s(\infty)=KE\),

  • Temps de réponse à \(\pm 5\%\) : Pas de formule simple. Lorsque \(m\gg 1\), le temps de réponse est dicté par le pôle le plus lent c-a-d \(t_r\approx -\frac{3}{p_1}\),

  • Pas de dépassement : \(s(\infty)=\max(s(t))=KE\).

Cas où \(m<1\)#

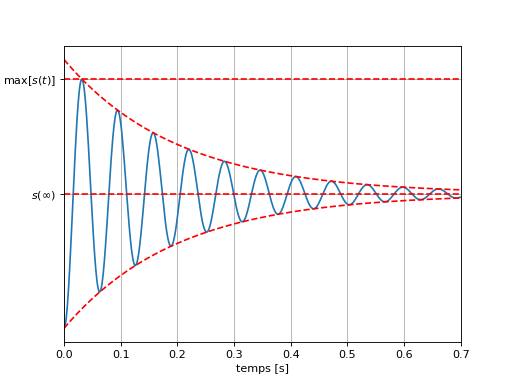
La figure suivante présente l’allure de la réponse indicielle lorsque \(m<1\). Dans ce contexte, la réponse présente un dépassement plus ou moins important et des oscillations de pseudo-pulsation \(\omega_p\). Pour analyser les performances d’un système de second ordre lorsque \(m<1\), nous utilisons principalement des abaques.

../../_images/second_order-3.png

La réponse indicielle s’exprime sous la forme :

\[s(t)=KE\left(1-\frac{1}{\sqrt{1-m^2}}e^{-m\omega_nt}\cos\left(\omega_n\sqrt{1-m^2}t-\arcsin(m)\right)\right)u(t)\]

Propriétés

  • Valeur initiale : \(s(0)=0\),

  • Valeur finale : \(s(\infty)=KE\),

  • Temps de réponse à \(\pm 5\%\) : Pas de formule simple, nous utiliserons des abaques. Lorsque \(m\to 0\), le temps de réponse est approximativement imposé par l’enveloppe c-a-d \(t_r\approx \frac{3}{\omega_n m}\),

  • Présence d’oscillations à la pseudo-pulsation (rad/s):

\[\omega_p = \omega_n\sqrt{1-m^2}\]

  • Premier Dépassement relatif :

\[D_r(\%)=100\times \frac{\max[s(t)]-s(\infty)}{s(\infty)} =100\times e^{\frac{-\pi m}{\sqrt{1-m^2}}}\]

Note

En pratique, nous utiliserons des abaques pour déterminer le temps de réponse et le premier dépassement relatif : https://vincentchoqueuse.github.io/ENIB_tools/control_settling_time.html

Identification#

Lorsque \(m<1\), l’identification graphique des paramètres peut s’obtenir de la manière suivante:

  • Gain statique: le gain statique s’obtient à partir de la valeur finale via la relation \(K = s(\infty)/E\).

  • Coefficient d’amortissement: le coefficient d’amortissement s’obtient en mesurant la valeur du premier dépassement relatif et en utilisant l’abaques donnant \(D_r(\%)\) en fonction de \(m\).

  • Pulsation propre: la pulsation propre s’obtient en mesurant la valeur du temps de réponse à \(\pm 5\%\) et en utilisant la valeur de \(m\) ainsi que l’abaque donnant \(\omega_n t_r = f(m)\).

Réponse Fréquentielle#

La réponse fréquentielle s’obtient en posant \(p=j\omega\) où \(\omega\) désigne la pulsation (en rad/s). La réponse fréquentielle d’un système passe-bas de premier ordre est donnée par :

\[H(j\omega)=\frac{K}{1-\frac{\omega^2}{\omega_n^2}+j\frac{2m\omega }{\omega_n}}\]

Module#

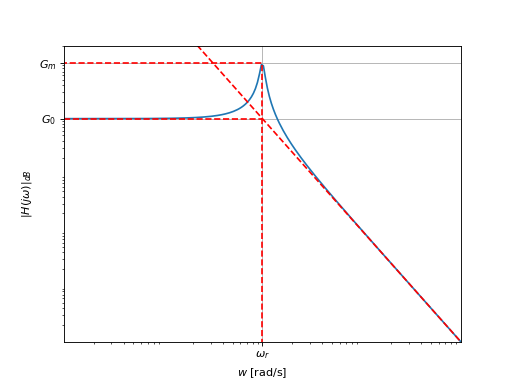
La figure suivante présente l’allure le module de la réponse fréquentielle. Lorsque \(m<0.7\), le module présente un maximum à la pulsation de résonance \(\omega_r\).

../../_images/second_order-4.png

Le module s’exprime sous la forme

\[|H(j\omega)|=\frac{|K|}{\sqrt{\left(1-\frac{\omega^2}{\omega_n^2}\right)^2+\frac{4m^2\omega^2}{\omega_n^2}}}\]

Propriétés

  • Amplification basse-fréquence : \(\lim_{\omega\to 0}|H(j\omega)|=|K|\),

  • Amplification haute-fréquence : \(\lim_{\omega\to \infty}|H(j\omega)|=0\),

  • Comportement asymptotique : Pour \(\omega \gg \omega_n\), \(|H(j\omega)|\approx |K| \left(\frac{\omega}{\omega_n}\right)^{-2}\) (pente de -2),

Si \(m<\frac{1}{\sqrt{2}}\approx 0.7\), il est possible de montrer que la dérivée du module présente un zéro. Dans ce contexte, le module présente un extremum nommé résonance.

  • Pulsation de résonance :

\[\omega_r = \omega_n \sqrt{1-2m^2}\]

  • Maximum du module : le maximum est égal à \(|H(j\omega_r)|=|K|/(2m\sqrt{1-m^2})\). En pratique, nous utiliserons essentiellement le facteur de resonance \(M\) qui s’obtient en divisant le module à la pulsation de résonance par le module du gain statique c-à-d

\[M=\frac{|H(j\omega_r)|}{|K|}=\frac{1}{2m\sqrt{1-m^2}}\]

En dB, le facteur de résonance s’exprime sous la forme

\[M_{dB} = G_{m} - G_{0}\]

  • \(G_{m} = 20 \log_{10}(|H(j\omega_r)|)\) correspond au module à la pulsation de résonance en dB,

  • \(G_{0} = 20 \log_{10}(|K|)\) correspond au module du gain statique en dB.

Note

En pratique, nous utiliserons des abaques pour déterminer le facteur de résonance en dB : https://vincentchoqueuse.github.io/ENIB_tools/control_resonance.html

Argument#

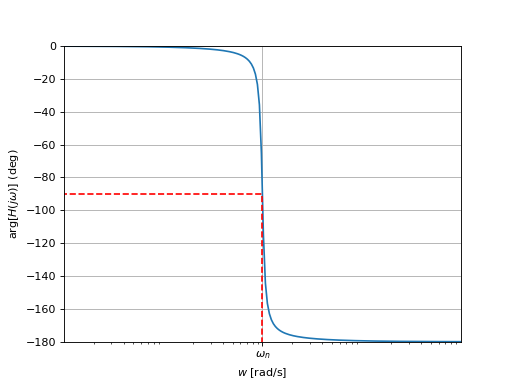
../../_images/second_order-5.png

Lorsque \(K>0\), l’argument s’exprime sous la forme

\[\arg[H(j\omega)]=-\textrm{arctan}\left(\frac{1}{2m} \left( \frac{\omega}{\omega_n} - \frac{\omega_n}{\omega}\right) \right) - \frac{\pi}{2}\]

Propriétés

Si \(K>0\), nous obtenons les propriétés suivantes.

  • Déphasage basse-fréquence : \(\lim_{\omega\to 0}\arg[H(j\omega)]=0\),

  • Déphasage haute-fréquence : \(\lim_{\omega\to \infty}\arg[H(j\omega)]=-180^o\).

  • Déphasage à la pulsation propre : \(\arg[H(j\omega_n)]=-90^o\).

Identification#

L’identification graphique des paramètres peut s’obtenir de la manière suivante:

  • Gain statique: le gain statique correspond à la valeur du module en basse-fréquence. Si le module est affiché en dB, la valeur du module s’obtient via l’expression \(K = 10^{G_0/20}\). Attention à bien vérifier que la phase évolue de \(0\) à \(-180^o\). Si ca n’est pas le cas, le gain est négatif.

  • Coefficient d’amortissement: le coefficient d’amortissement s’obtient en mesurant le facteur de résonance \(M_{dB}\) et en utilisant l’abaque donnant le facteur de résonance en dB en fonction de \(m\).

  • Pulsation propre: la pulsation propre peut s’obtenir de deux façons.

    • Si la phase est disponible, la pulsation propre s’obtient en déterminant la pulsation telle que \(\arg[H(j\omega)] = -90^o\) (lorsque \(K\) est positif).

    • Si la phase n’est pas disponible, la pulsation propre s’obtient à partir de la valeur de \(m\) et de la mesure de la pulsation résonance \(\omega_r\), puis en utilisant la relation \(\omega_r = \omega_n \sqrt{1-2m^2}\).