Systèmes Echantillonnés

Contexte

Dans ce chapitre, nous montrons comment utiliser la transformée en Z pour analyser un système composé de CNA, d’un système continu et d’un CAN. Pour modéliser l’effet du CNA, nous introduisons le bloqueur d’ordre 0. Nous montrons ensuite qu’il est possible d’obtenir facilement la fonction de transfert en Z du système composé d’un CNA avec bloqueur d’ordre 0, d’un système analogique de fonction de transfert \(F(p)\) et d’un CAN.

Modélisation CNA/CAN avec BOZ

Même si la correction se fait en numérique, en pratique, le système à contrôler reste le plus souvent analogique. Pour pouvoir mettre en place une stratégie de correction, il est alors nécessaire de modéliser l’influence des convertisseurs A/N et N/A.

Soit un système comportant

• un CNA de période d’échantillonnage \(T_e\),

• le système continu \(F(p)\),

• un CAN de période d’échantillonnage \(T_e\) modélisé par un bloqueur d’ordre 0 (BOZ)

CNA avec BOZ

Bloqueur d’ordre 0

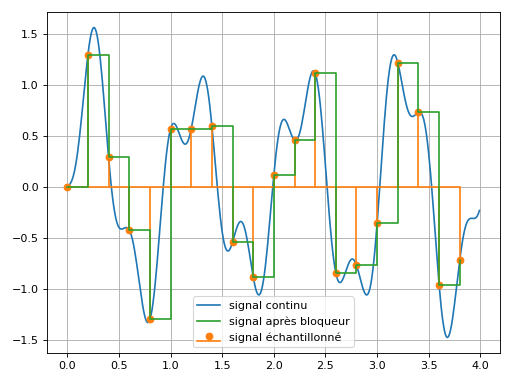
Le bloqueur d’ordre 0 permet d’obtenir un signal analogique à partir d’un signal numérique. Spécifiquement, le bloqueur d’ordre 0 “bloque” la valeur du signal entre deux instants d’échantillonnage.

Un bloqueur d’ordre 0 peut être modélisé par un filtre analogique de réponse impulsionnelle

\[\begin{split}h(t) = u(t)-u(t-T_e) =\left\{\begin{array}{cl}1 & \text{ si }0\le t \le T_e \\ 0&\text{ ailleurs}\end{array}\right.\end{split}\]

La fonction de transfert du bloqueur d’ordre 0 est alors donnée par

\[B_0(p) = \mathcal{L}[h(t)]=\frac{1}{p}-\frac{e^{-pT_e}}{p}=\frac{1-e^{-pT_e}}{p}\]

Fonction de transfert

La chaîne composée du CNA avec BOZ, du système continu et du CAN peut être modélisée par la fonction de transfert en Z suivante

\[F(z)=\frac{z-1}{z}TZ\left[TL^{-1}\left[\frac{F(p)}{p}\right]\right]\]

Dans la plupart des cas, nous utiliserons par abus de notation la relation suivante :

\[F(z)=\frac{z-1}{z}TZ\left[\frac{F(p)}{p}\right]\]

Demonstration

En utilisant directement l’abus de notation, la fonction de transfert d’une chaine CNA/CAN avec BOZ s’exprime sous la forme

\[\begin{split}F(z)&= TZ\left[B_0(p)F(p)\right]\\ &=TZ\left[\frac{F(p)}{p}\right]-TZ\left[\frac{(e^{-pT_e}F(p)}{p}\right]\\ &=TZ\left[\frac{F(p)}{p}\right]-z^{-1}TZ\left[\frac{F(p)}{p}\right]\\ &=(1-z^{-1}) TZ\left[\frac{F(p)}{p}\right]\\ &=\frac{z-1}{z}TZ\left[\frac{F(p)}{p}\right]\end{split}\]

Propriétés

• Les gains statiques de \(F(z)\) et de \(F(p)\) sont identiques.

• Les pôles de la fonction de transfert \(F(z)\) sont liés aux pôles de \(F(p)\) par la relation

\[z_k = e^{p_kT_e}\]

Exemple

Considérons un système continu de premier ordre de fonction de transfert

\[F(p)=\frac{K}{1+\tau p}\]

Le pôle du système est donné par \(p=-\frac{1}{\tau}\).

La Fonction de transfert discrete du système composée du CNA avec BOZ, de \(F(p)\) et d’un CAN est égale à

\[F(z)=K\left(\frac{1-e^{-\frac{T_e}{\tau}}}{z-e^{-\frac{T_e}{\tau}}} \right)\]

où \(T_e\) désigne la période d’échantillonnage. Nous remarquons bien que le gain statique de \(F(z)\) est égal à \(F(1)=K\). De plus, nous observons que \(F(z)\) possède un unique pôle en \(z=e^{p T_e}\) où \(p=-\frac{1}{\tau}\) correspond au pôle du système continu.