Systèmes de Second Ordre#

Modélisation#

Equation différentielle#

\[\frac{1}{\omega_0^2}\frac{d^2 s(t)}{dt^2} +\frac{2m}{\omega_0}\frac{d s(t)}{dt}+s(t) = b_2\frac{d^2 e(t)}{dt^2} +b_1\frac{d e(t)}{dt}+b_0 e(t)\]

  • \(\omega_0\) désigne la pulsation propre [rad/s],

  • \(m\) le coefficient d’amortissement.

Fonction de transfert#

La fonction de transfert d’un système de second ordre peut s’exprimer sous la forme normalisée suivante :

\[H(p)=\frac{N(p)}{\frac{1}{\omega_0^2}p^2+\frac{2m}{\omega_0}p+1}\]

  • \(N(p)\) désigne le numérateur de la fonction de transfert (polynôme de degré inférieur ou égale à 2).

Exemples#

\[\begin{split}H_{LP}(p)&=\frac{T_0}{\frac{1}{\omega_0^2}p^2+\frac{2m}{\omega_0}p+1}\\ H_{BP}(p)&=\frac{\frac{2mT_m}{\omega_0}p}{\frac{1}{\omega_0^2}p^2+\frac{2m}{\omega_0}p+1}​\\ H_{HP}(p)&=\frac{\frac{T_{\infty}}{\omega_0^2}p^2}{\frac{1}{\omega_0^2}p^2+\frac{2m}{\omega_0}p+1}​\\ H_{BR}(p)&=\frac{T_0\left(\frac{1}{\omega_0^2}p^2+1\right)}{\frac{1}{\omega_0^2}p^2+\frac{2m}{\omega_0}p+1}​\end{split}\]

Expressions des Pôles#

Les pôles s’obtiennent en déterminant les racines du dénominateur de la fonction de transfert c-a-d en déterminant les valeurs de \(p\) telles que :

\[\frac{1}{\omega_0^2}p^2+\frac{2m}{\omega_0}p+1 = 0\]

Cette équation est une équation du second degré. Le discriminant s’exprime sous la forme suivante:

\[\Delta = \left(\frac{2m}{\omega_0}\right)^2-\frac{4}{\omega_0^2} =\frac{4}{\omega_0^2}\left(m^2-1\right)\]

L’expression du discriminant montre que la valeur de m joue un rôle essentiel dans l’expression des deux racines. Nous pouvons distinguer 3 cas de figure.

Cas où m>1#

Lorsque \(m>1\), le système possède deux poles réels et distincts. Les pôles s’expriment sous la forme

\[\begin{split}p_1 = -m\omega_0 +\omega_0 \sqrt{m^2-1}\\ p_2 = -m\omega_0 -\omega_0 \sqrt{m^2-1}\end{split}\]

Mathématiquement, nous obtenons les propriétés suivantes:

  • le produit des deux pôles est égale à \(p_1p_2=m^2\omega_0^2-\omega_0^2(m^2-1)=\omega_0^2\)

  • la somme des deux pôle est égale à \(p_1+p_2=-2m\omega_0\).

Nous en déduisons alors que:

\[\begin{split}\omega_0 &= \sqrt{p_1p_2}\\ m &= -\frac{p_1+p_2}{2\omega_0}\end{split}\]

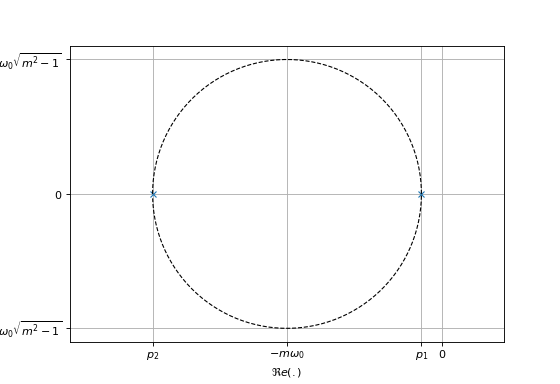
Géométriquement, les deux pôles sont placés sur un cercle de centre \(-m\omega_0\) et de rayon \(\omega_0\sqrt{m^2-1}\).

../_images/second_order-1.png

Cas où m=1#

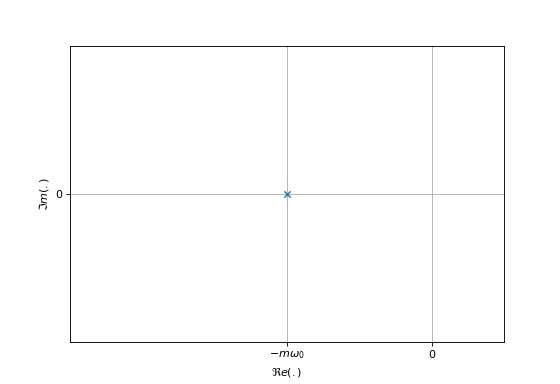
Lorsque \(m=1\), le système possède un pole réel double. Le pole réel double s’exprime sous la forme

\[p_1 = p_2 = -m\omega_0\]
../_images/second_order-2.png

Cas où m<1#

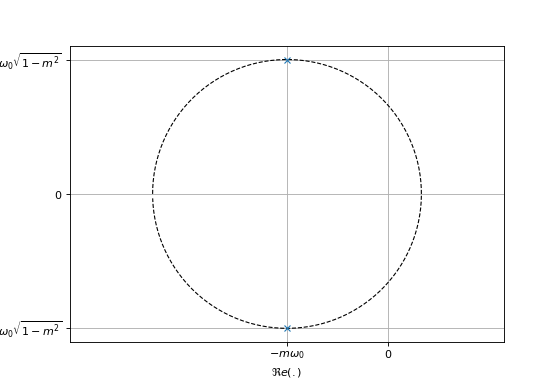
Lorsque \(m<1\), le système possède une paire de pôles complex-conjugués. Les pôles s’expriment sous la forme

\[\begin{split}p_1 = -m\omega_0 +j\omega_0 \sqrt{1-m^2}\\ p_2 = -m\omega_0 -j\omega_0 \sqrt{1-m^2}\end{split}\]

Mathématiquement,

  • le module de chaque pôle est égal à \(|p_1|=|p_2|=\sqrt{(m\omega_0)^2+\omega_0^2(1-m^2)}=\omega_0\).

  • l’angle formé entre le pôle \(p_1\) et l’axe des réels est donné par \(\cos(\theta)=-\Re e(p_1)/|p_1|=m\)

Nous en déduisons alors que:

\[\begin{split}\omega_0 &= \sqrt{p_1p_1^*}=|p_1|\\ m &= -\frac{\Re e(p_1)}{\omega_0 }\end{split}\]
../_images/second_order-3.png

Réponse Temporelle#

La réponse à une entrée quelconque s’exprime sous la forme :

\[s(t) = s_l(t) + s_p(t)\]

  • \(s_l(t)\): solution libre,

  • \(s_p(t)\): solution particulière.

Cas où m>1#

Le régime libre s’exprime sous la forme :

\[s_l(t)=\lambda_1 e^{-(m-\sqrt{m^2-1})\omega_0t}+\lambda_2 e^{-(m+\sqrt{m^2-1})\omega_0t}\]

Le régime libre est donné par la contribution de deux systèmes de premier ordre ayant pour constantes de temps respectives:

\[\tau_{1,2} =-\frac{1}{p_{1,2}}=\frac{1}{\omega_0 (m\pm \sqrt{m^2-1})}\]

Cas où m<1#

Le régime libre s’exprime alors sous la forme :

\[s_l(t)=\lambda e^{-m\omega_0t}\cos(\omega_0 \sqrt{1-m^2}t+\varphi)\]

  • \(-m\omega_0`\) régit la vitesse de décroissance de l’enveloppe,

  • \(\omega_p=\omega_0 \sqrt{1-m^2}\) correspond à la pseudo-pulsation des oscillations [rad/s]

Propriétés#

  • Oscillations : pseudo-pulsation et pseudo-période.

\[\begin{split}\omega_p &=\omega_0\sqrt{1-m^2}\\ T_p &= \frac{2\pi}{\omega_0\sqrt{1-m^2}}\end{split}\]

  • Ratio des amplitudes après une oscillation :

\[R = \frac{s_l(t_1)}{s_l(t_1+T_p)}=e^\frac{2\pi m}{\sqrt{1-m^2}} > 1\]

Lorsque \(m\ll 1\), \(\omega_p\approx \omega_0\) et \(R\approx e^{2\pi m}\).

Réponse Indicielle#

  • Comportement à la discontinuité : Pour les signaux ne présentant pas de singularité au voisinage de 0, il est possible d’établir que (voir démonstration) :

\[\begin{split}\Delta s(0) &= \omega_0^2 b_2 \Delta e(0) \\ \Delta \dot{s}(0) &= (b_1 \omega_0^2-2m b_2 \omega_0^3)\Delta e(0)+b_2 \omega_0^2\Delta \dot{e}(0)\end{split}\]

  • Regime permanent : Lorsque l’entrée est un échelon, la sortie en régime permanent s’exprime sous la forme

\[s(\infty) = b_0 E\]

Formes Normalisées#

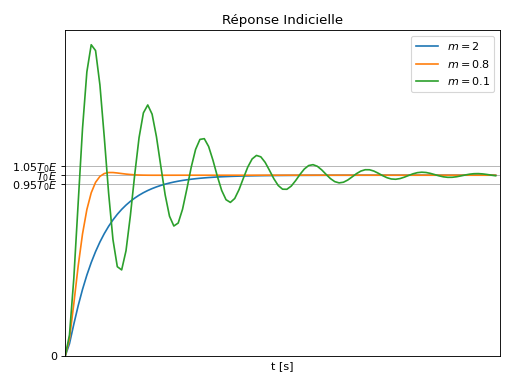
Passe-bas (LP)#

\[H(p)=\frac{T_0}{\frac{1}{\omega_0^2}p^2+\frac{2m}{\omega_0}p+1}​\]

  • gain statique: \(T_0\),

  • pulsation propre: \(\omega_0\) (rad/s),

  • coefficient d’amortissement: \(m\).

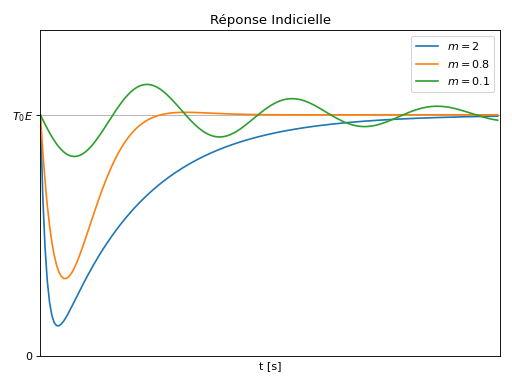
Réponse Indicielle

../_images/second_order-4.png

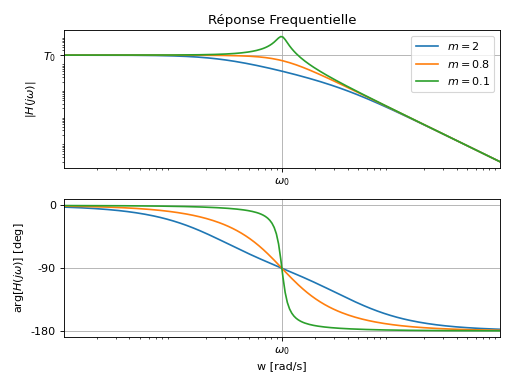
Comportement Fréquentiel

  • Valeur à la pulsation propre: \(H(j\omega_0)=\frac{T_0}{2jm}\),

  • Si \(m<0.7\), présence d’une résonance à la pulsation \(\omega_r=\omega_0\sqrt{1-2m^2}\) [rad/s]

\[|H(j\omega_r)|=\frac{T_0}{2m\sqrt{1-m^2}}\]
../_images/second_order-5.png

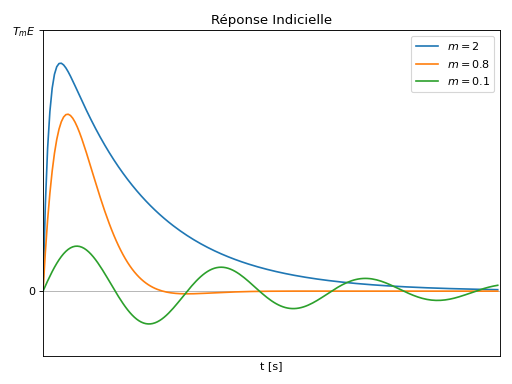
Passe-bande (BP)#

\[H(p)=\frac{\frac{2mT_m}{\omega_0}p}{\frac{1}{\omega_0^2}p^2+\frac{2m}{\omega_0}p+1}​\]

  • gain maximum: \(T_m\),

  • pulsation propre: \(\omega_0\) (rad/s),

  • coefficient d’amortissement: \(m\).

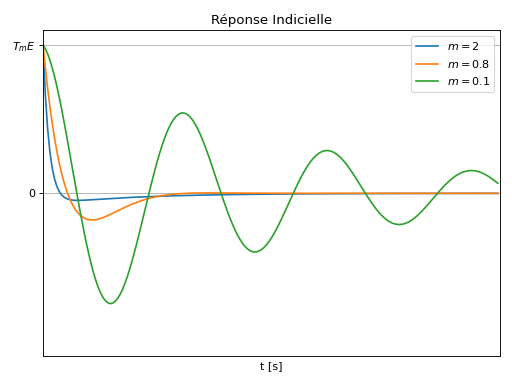
Réponse Indicielle

../_images/second_order-6.png

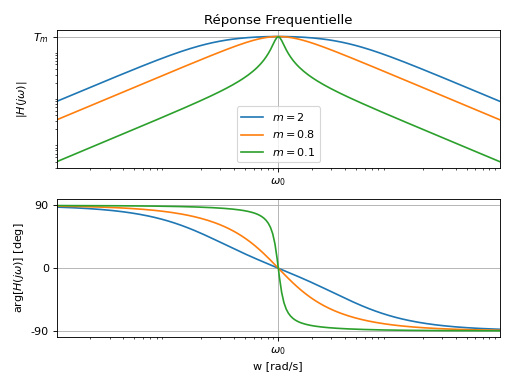
Comportement Fréquentiel

  • Valeur à la pulsation propre: \(H(j\omega_0)=T_m\),

  • Intersection des asymptotes de module: \(T_i=2m T_m\),

  • Largeur de la bande passante à -3dB: \(\Delta \omega =2m \omega_0\) [rad/s].

../_images/second_order-7.png

Passe-haut (HP)#

\[H(p)=\frac{\frac{T_{\infty}}{\omega_0^2}p^2}{\frac{1}{\omega_0^2}p^2+\frac{2m}{\omega_0}p+1}​\]

  • gain haute-fréquence: \(T_{\infty}\),

  • pulsation propre: \(\omega_0\) (rad/s),

  • coefficient d’amortissement: \(m\).

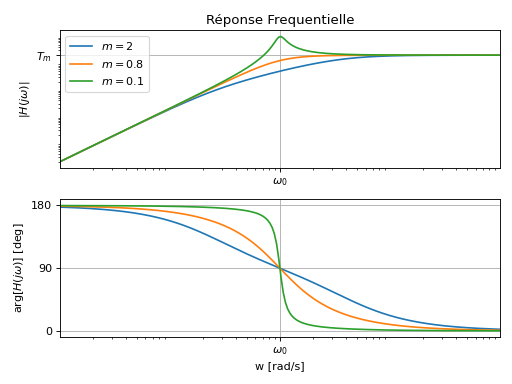
Réponse Indicielle

../_images/second_order-8.png

Comportement Fréquentiel

  • Valeur à la pulsation propre: \(H(j\omega_0)=j\frac{T_{\infty}}{2m}\),

  • Si \(m<0.7\), présence d’une résonance à la pulsation \(\omega_r=\omega_0/\sqrt{1-2m^2}\) [rad/s]

\[|H(j\omega_r)|=\frac{T_{\infty}}{2m\sqrt{1-m^2}}\]
../_images/second_order-9.png

Rejecteur (Notch)#

\[H(p)=\frac{T_0\left(\frac{1}{\omega_0^2}p^2+1\right)}{\frac{1}{\omega_0^2}p^2+\frac{2m}{\omega_0}p+1}​\]

  • gain maximum: \(T_0\),

  • pulsation propre: \(\omega_0\) (rad/s),

  • coefficient d’amortissement: \(m\).

Réponse Indicielle

../_images/second_order-10.png

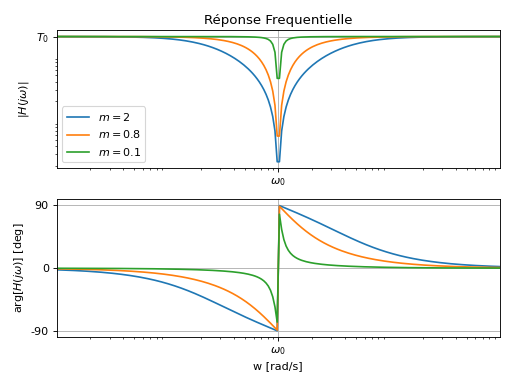
Comportement Fréquentiel

  • Valeur à la pulsation propre: \(H(j\omega_0)=0\),

  • Largeur de la bande rejetée à -3dB: \(\Delta \omega =2m \omega_0\) [rad/s].

../_images/second_order-11.png