Expression de la valeur initiale#

Introduction#

Lorsqu’un système est excité par une entrée \(e(t)\) en \(t=0^+\), la sortie \(s(t)\) peut présenter différents comportements. Ces différents comportements permettent d’identifier le type de filtre (passe-bas, passe-haut, etc) et certains paramètres.

Dans ce tutorial, nous nous intéressons spécifiquement au comportement à l’excitation, c-à-d en \(t=0^+\).

Pour analyser le comportement en \(t=0^+\), ce tutorial présente une solution basée sur l’équation différentielle. Pour des raisons de simplicité, les approches présentées ci dessous se limitent au cas des systèmes de second ordre.

Approche Temporelle#

Considérons un système de second ordre décrit par l’équation différentielle suivante

\[a_2 \ddot{s}(t)+a_1 \dot{s}(t)+a_0 s(t)=b_2 \ddot{e}(t)+b_1 \ddot{e}(t)+b_0 e(t)\]

Dans les développements qui suivent nous allons considérer que les signaux d’entrée et de sortie n’a pas de comportement “singulier” ou infini en 0. Mathématiquement, cela implique que :

\[\int_{0^-}^{0+} e(t) dt = \int_{0^-}^{0+} e(t) dt = 0\]

Note

Remarquons que la méthodologie décrite ci dessous ne permet pas d’obtenir la réponse implulsionnelle pour laquelle \(e(t)=\delta(t)\).

Valeur Initiale#

Il est possible de trouver la valeur initiale en \(t=0^+\) en intégrant plusieurs fois l’équation différentielle par rapport à \(t\), et en évaluant le résultat entre \(0^-\) et \(0^+\).

Intégration Simple#

En intégrant une fois l’équation différentielle entre \(0^-\) et \(0^+\), nous obtenons :

\[a_2 \int_{0^-}^{0^+}\ddot{s}(t)dt+a_1 \int_{0^-}^{0^+}\dot{s}(t)dt +a_0 \int_{0^-}^{0^+}s(t)dt=b_2 \int_{0^-}^{0^+}\ddot{e}(t)dt+b_1 \int_{0^-}^{0^+}\dot{e}(t)dt+b_0 \int_{0^-}^{0^+}e(t)dt\]

En supposant que l’entrée et la sortie ne contiennent pas d’impulsion, nous trouvons :

\[a_2 \left[\dot{s}(t)\right]_{0^-}^{0^+}+a_1 \left[s(t)\right]_{0^-}^{0^+} =b_2 \left[\dot{e}(t)\right]_{0^-}^{0^+}+b_1 \left[e(t)\right]_{0^-}^{0^+}\]

et donc :

\[a_2 \left(\dot{s}(0^+)-\dot{s}(0^-)\right)+a_1 \left(s(0^+)-s(0^-)\right) =b_2 \left(\dot{e}(0^+)-\dot{e}(0^-)\right)+b_1 \left(e(0^+)-e(0^-)\right)\tag{1}\]

Intégrations successives#

En intégrant deux fois l’équation différentielle entre \(0^-\) et \(0^+\), nous obtenons :

\[\begin{split}a_2 \int_{0^-}^{0^+}\int\ddot{s}(t)dt^2+a_1 \int_{0^-}^{0^+}\int\dot{s}(t)dt^2 +a_0 \int_{0^-}^{0^+}\int s(t)dt^2\\ =b_2 \int_{0^-}^{0^+} \int\ddot{e}(t)dt^2+b_1 \int_{0^-}^{0^+} \int\dot{e}(t)dt^2+b_0 \int_{0^-}^{0^+} \int e(t)dt^2\end{split}\]

En supposant que l’entrée et la sortie ne contiennent pas d’impulsion, les deux derniers termes des deux membres sont nuls. Dans ce contexte, l’égalité se simplifie sous la forme :

\[a_2 \left[s(t)\right]_{0^-}^{0^+}=b_2 \left[e(t)\right]_{0^-}^{0^+}\]

et donc :

\[a_2(s(0^+)-s(0^-)) = b_2(e(0^+)-e(0^-))\tag{2}\]

Modélisation matricielle#

Ces relations permettent de définir un système d’équation. Pour simplifier la résolution du système, il est possible d’utiliser une notation matricielle. Définissons tout d’abord les vecteurs suivants :

\[\begin{split}\mathbf{s}(t) &= \begin{bmatrix} s(t) \\ \dot{s}(t)\end{bmatrix} \\ \mathbf{e}(t) &= \begin{bmatrix} e(t) \\ \dot{e}(t)\end{bmatrix}\end{split}\]

ainsi que les vecteurs de “variation”

\[\begin{split}\Delta\mathbf{s}(t) &= \mathbf{s}(t^+)-\mathbf{s}(t^-) = \begin{bmatrix} s(t^+)- s(t^-)\\ \dot{s}(t^+)-\dot{s}(t^-)\end{bmatrix} \\ \Delta \mathbf{e}(t) &= \mathbf{e}(t^+)-\mathbf{e}(t^-) = \begin{bmatrix} e(t^+)-e(t^-) \\ \dot{e}(t^+)-\dot{e}(t^-)\end{bmatrix}\end{split}\]

En exploitant ces notations et les équations (1) et (2), nous obtenons le système

\[\begin{split}\begin{bmatrix}a_2 & 0 \\ a_1 &a_2\end{bmatrix}\Delta\mathbf{s}(0) = \begin{bmatrix}b_2 & 0 \\ b_1 &b_2 \end{bmatrix}\Delta\mathbf{e}(0)\end{split}\]

En utilisant le fait que

\[\begin{split}\begin{bmatrix}a_2 & 0 \\ a_1 &a_2\end{bmatrix}^{-1} = \frac{1}{a_2^2}\begin{bmatrix}a_2 & 0 \\ -a_1 &a_2\end{bmatrix},\end{split}\]

le vecteur \(\Delta\mathbf{s}(0)\) peut s’exprimer sous la forme

\[\begin{split}\Delta\mathbf{s}(0) = \frac{1}{a_2^2}\begin{bmatrix}a_2 & 0 \\ -a_1 &a_2\end{bmatrix}\begin{bmatrix}b_2 & 0 \\ b_1 &b_2 \end{bmatrix}\Delta\mathbf{e}(0)\end{split}\]

Nous obtenons finalement

\[\begin{split}\Delta\mathbf{s}(0) = \frac{1}{a_2^2}\begin{bmatrix}a_2b_2 & 0 \\ a_2b_1-a_1b_2 &a_2 b_2 \end{bmatrix} \Delta\mathbf{e}(0)\end{split}\]

Exemples#

Dans cette partie, nous nous intéressons aux comportements des filtres de second ordre de type passe-bas, passe-bande, passe-haut et rejecteur. les

Pour ces filtres, nous obtenons la relation générale :

\[\begin{split}\Delta\mathbf{s}(0) = \omega_0^2\begin{bmatrix} b_2 & 0 \\ b_1 -2m b_2 \omega_0 & b_2 \end{bmatrix} \Delta\mathbf{e}(0)\end{split}\]

Propriétés#

  • Passe-bas :

\[\begin{split}\Delta s(0) &= 0\\ \Delta \dot{s}(0) & =0\end{split}\]

  • Passe-bande :

\[\begin{split}\Delta s(0) &= 0\\ \Delta \dot{s}(0) & =2m \omega_0 T_m \Delta e(0)\end{split}\]

  • Passe-haut :

\[\begin{split}\Delta s(0) &= T_{\infty}\Delta e(0)\\ \Delta \dot{s}(0) & =T_{\infty}\Delta \dot{e}(0)- 2m \omega_0 T_{\infty} \Delta e(0)\end{split}\]

  • Rejecteur :

\[\begin{split}\Delta s(0) &= T_{0}\Delta e(0)\\ \Delta \dot{s}(0) & =T_{0}\Delta \dot{e}(0)- 2m \omega_0 T_{0} \Delta e(0)\end{split}\]

Illustrations#

Considérons le cas où l’entrée est un échelon d’amplitude \(E=1\). Dans ce contexte, le vecteur d’entrée est égale à

\[\begin{split}\Delta\mathbf{e}(0)=\begin{bmatrix}1 \\ 0\end{bmatrix}\end{split}\]

La figure suivante présente la réponse indicielle pour un filtre passe-bas, passe-bande, passe-haut et rejecteur ayant la même pulsation propre \(\omega_0=1\) rad/s, le même coefficient d’amortissement \(m=0.5\) et le même coefficient d’amplification \(T_0=T_\infty=T_m=2\).

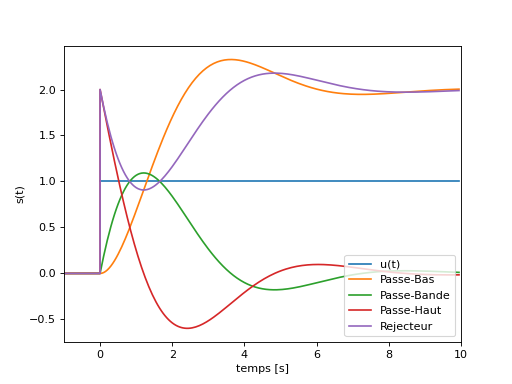
../_images/initial_values-1.png

Nous observons rapidement que :

  • Seuls les filtres passe-haut et rejecteur laissent passer les discontinuités en entrée.

  • Seuls les filtres passe-bas et rejecteur possèdent un regime permanent non nul.