Synthèse d’un filtre passe-bande#

Ce tutorial montre le process complet pour synthétiser un filtre d’ordre N à partir d’un cahier des charges. La méthodologie décrite ici est applicable à n’importe quel filtre.

Cahier des charges#

  • Type de filtre: passe-bande,

  • Technique de synthèse: Butterworth,

  • Bande passante : \(\omega \in [900, 1111]\) rad/s,

  • Bande rejetée : \(\omega \in [0, 500[ \cup [2000, +\infty[\) rad/s,

  • Atténuation maximale dans la bande passante: \(3\) dB,

  • Atténuation minimale dans la bande rejetée: \(40\) dB.

Détermination du Gabarit Normalisé#

Dans un premier temps, nous allons revenir à la conception d’un filtre passe-bas normalisé (\(\omega_c=1\) rad/s). Pour réaliser cette étape de normalisation, nous allons utiliser la formule liant la pulsation normalisée \(\omega\) et la pulsation dénormalisée \(\widehat{\omega}\) (voir Mapping Fréquentiel)

\[\omega = \frac{\widehat{\omega}^2-\omega_0^2}{\widehat{\omega}\Delta \omega}\]

Application Numérique#

  • Bande passante: \(\Delta \omega=1111-900=211\) rad/s.

  • Pulsation centrale : \(\omega_0=\sqrt{900\times 1111}=1000\) rad/s.

  • Valeur du module en \(\widehat{\omega}=1111\) rad/s: \(T_c=10^{-3/20}=0.707\),

  • Valeur du module en \(\widehat{\omega}=2000\) rad/s: \(T_s=10^{-40/20}=0.01\).

En utilisant la formule, nous obtenons :

\[\begin{split}\omega_c &= \frac{1111^2-1000^2}{1111\times 211}\approx 1~rad/s\\ \omega_s &= \frac{2000^2-1000^2}{2000\times 211}\approx 7.11~rad/s\\\end{split}\]

Représentation du Gabarit#

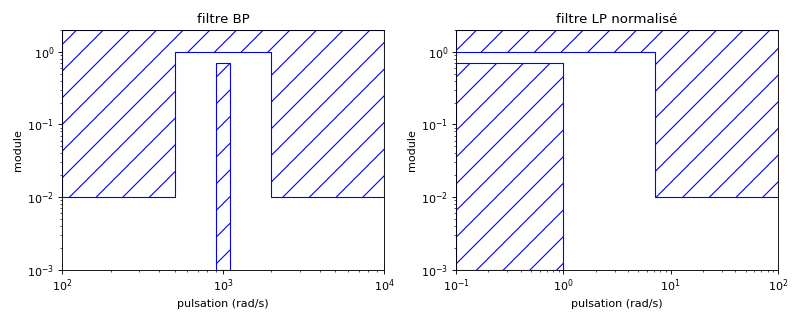
../_images/BP_design-1.png

Détermination de l’ordre#

Il est possible de déterminer l’ordre du filtre passe-bas normalisé en utilisant le comportement asymptotique :

\[N = \left\lceil-\frac{\ln\left(\frac{0.707}{0.01}\right)}{\ln\left(\frac{1}{7.11}\right)}\right\rceil = 3\]

Synthèse du Filtre Normalisé#

Pour synthétiser le filtre, nous allons utiliser la technique de synthèse de Butterworth. La fonction de transfert du filtre normalisé peut s’exprimer sous la forme factorisée suivante (zpk):

\[H_n(p)=k\frac{\prod_{l=1}^3 (p-z_l)}{\prod_{l=1}^3 (p-p_l)}\]

Il est possible d’obtenir les pôles \(p_l\) et les zéros \(z_l\) ainsi que le gain k du filtre normalisé en utilisant scipy:

from scipy.signal import butter

z,p,k = butter(3, 1, "low", analog=True, output="zpk")

Nous obtenons les paramètres suivants:

  • zéros: \(z_l=\{\}\),

  • pôles: \(p_l=\{-0.5+0.8660254, -1, -0.5-0.8660254j\}\),

  • gain: \(k=1\)

Dénormalisation du Filtre#

Pour dénormaliser le filtre, nous allons opérer un mapping des pôles et zéros. Dans le cas d’un passe-bande, le mapping des pôles est donné par (voir Mapping des pôles et zéros).

\[\begin{split}\widehat{p}_l&=\alpha p_l \pm \sqrt{\alpha^2p_l^2-\omega_0^2}\\\end{split}\]

  • \(\alpha=\Delta \omega/2=211/2=105.5\) rad/s désigne la moitié de la bande passante,

  • \(p_l\) correspond aux pôles du filtre normalisé,

  • \(\widehat{p}_l\) correspond aux pôles du filtre dénormalisé.

Après dénormalisation, nous obtenons un filtre d’ordre \(2N=6\). Pour conserver un gain maximum unitaire dans la bande passante, il est également nécessaire de changer le coefficient \(k\) de la manière suivante:

\[\widehat{k} = k (\Delta \omega)^N\]

Application Numérique#

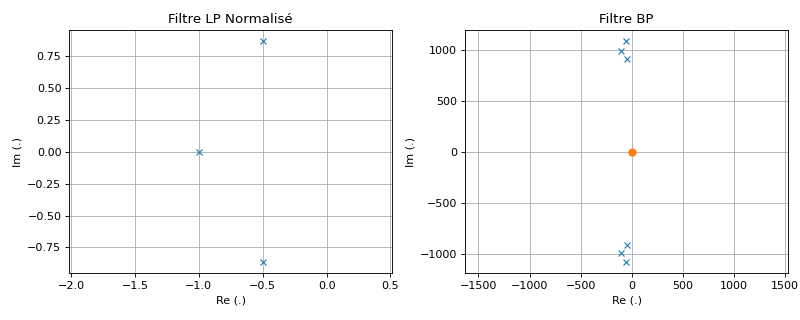
Après dénormalisation, nous obtenons un filtre d’ordre 6 avec les paramètres suivants :

  • zéros: 3 zéros en 0 (filtre passe-bande d’ordre 6)

    • \(\widehat{z}_l=\{0, 0, 0\}\),

  • pôles: 3 paires de pôles complexes-conjugués

    • \(\widehat{p}_1=-47.943-911.424j\) et \(\widehat{p}_1^*=-47.943+911.424j\),

    • \(\widehat{p}_2=-57.556-1094.155j\) et \(\widehat{p}_2^*=-57.556+1094.155j\)

    • \(\widehat{p}_3=-105.5-994.419j\) et \(\widehat{p}_3^*=-105.5+994.419j\),

  • gain k:

    • \(\widehat{k} = 1 \times (211)^3 =9393931\)

../_images/BP_design-2.png

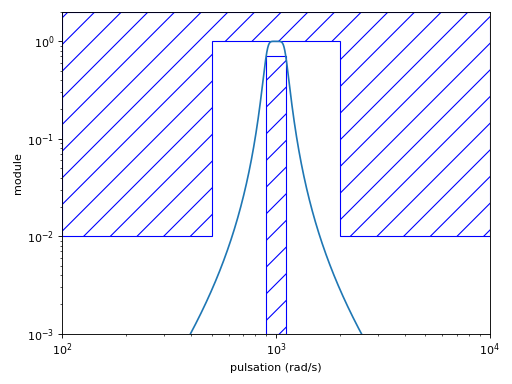
Vérification#

Pour vérifier que le filtre dénormalisé respecte bien les contraintes du cahier des charges, une solution naturelle consiste à afficher la réponse fréquentielle du filtre dénormalisé.

\[H(p)=\widehat{k}\frac{\prod_{l=1}^3 (p-\widehat{z}_l)}{\prod_{l=1}^6 (p-\widehat{p}_l)}\]
from scipy.signal import lti
import matplotlib.pyplot as plt

k2 = 9393931
z2 = [0.+0.j, 0.+0.j, 0.+0.j]
p2 = [ -47.943-911.374j, -105.5-994.369j, -47.943 +911.374j, -57.556+1094.106j, -105.5 +994.369j, -57.556-1094.106j]
H = lti(z2, p2, k2)
w, Hjw = H.freqresp()
plt.loglog(w, np.abs(Hjw))
plt.xlabel("pulsation (rad/s)")
plt.ylabel("module")
../_images/BP_design-3.png