Analyse d’un Circuit de Premier Ordre#

Dans ce tutorial, nous allons réaliser une analyse complète d’un circuit. Le circuit considéré est le suivant :

Fonction de Transfert#

La fonction de transfert du circuit s’obtient en utilisant le pont diviseur de tension. En notant \(s(t)\) la sortie \(V_{out}(t)\) et \(e(t)\) l’entrée \(V_{in}(t)\), nous obtenons dans le domaine de Laplace:

\[\begin{split}S(p) &= \frac{Z_c}{Z_c+Z_r} E(p) &= \frac{\frac{1}{Cp}}{\frac{1}{Cp}+R} S(p)\\ &= \frac{1}{RCp+1} E(p)\end{split}\]

Nous en déduisons que la fonction de transfert du système est égal à

\[H(p) = \frac{S(p)}{E(p)} = \frac{1}{RCp+1}\]

Pour specifier cette fonction de transfert en Python, nous allons utiliser la module scipy.

Réponse Temporelle#

Le système peut être décrit dans le domaine temporelle par l’équation suivante :

\[RC \frac{d s(t)}{dt} + s(t) = e(t)\]

Réponse Indicielle#

Nous allons nous intéresser à la sortie lorsque l’entrée est un échelon d’amplitude E

\[\begin{split}e(t) = \left\{\begin{array}{cc}E&\text{ si } t\ge 0\\ 0 &\text{ ailleurs} \end{array}\right.\end{split}\]

La sortie du système est supposée initialement nulle c-a-d \(s(0^-)=0\).

Expression#

Equation caractéristique :

\[RC p + 1 = 0 \Rightarrow p=-\frac{1}{RC}\]

Régime Libre :

\[s_l(t) = \lambda e^{-\frac{1}{RC} t}\]

Régime Forcé : Lorsque l’entrée est un échelon d’amplitude E, le regime permanent s’exprime sous la forme \(s_p(t) = S u(t)\). La valeur de \(S\) s’obtient en injectant l’expression du regime permanent dans l’équation différentielle. Pour \(t\ge 0\), nous obtenons :

\[s_p(t) = E\]

Solution Complète: Pour \(t\ge 0\), nous obtenons finalement

\[s(t) = s_l(t) + s_p(t) = \lambda e^{-\frac{1}{RC} t} + E\]

La détermination de la constante d’intégration peut s’obtenir en déterminant la valeur de \(s(t)\) en \(t=0^+\). Cette valeur peut s’obtenir en intégrant l’équation différentielle entre \(t=0^-\) et \(t=0^+\).

\[RC \int_{0^-}^{0^+}\frac{d s(t)}{dt} dt + \int_{0^-}^{0^+}s(t)dt= E \int_{0^-}^{0^+} 1 dt = 0\]

Sous l’hypothèse où la seconde intégrale du terme de gauche est nulle et en utilisant le fait que la sortie est initialement nulle, nous obtenons :

\[RC \left[s(t)\right]_{0^-}^{0^+} = 0 \Rightarrow s(0^+) = 0\]

En exploitant cette equation, il en vient que :

\[s(0^+) =\lambda \times 1 + E = 0 \Rightarrow \lambda = -E\]

Pour \(t\ge 0\), nous obtenons finalement l’expression suivante :

\[s(t) = E\left(1-e^{-\frac{1}{RC} t}\right)\]

Valeurs Remarquables#

Valeur initiale: \(s(0^+)=0\),
Valeur finale: \(s(\infty)=E\),
Valeur maximale: \(max(s(t))=E\),
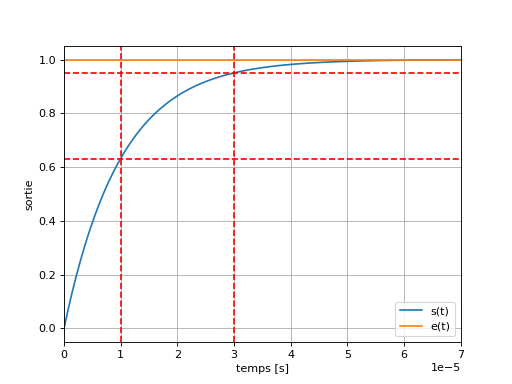
Valeur en \(t=\tau=RC\), \(s(\tau)=0.63E\),
Valeur en \(t=3\tau=3RC\), \(s(3\tau)=0.95E\).

Simulation Python#

import numpy as np
import matplotlib.pyplot as plt
from scipy.signal import lti, step

R = 10*(10**3)
C = 10**(-9)
num = [1]
den = [R*C, 1]
H = lti(num, den)


E = 1
t, s = step(H)
plt.plot(t, s, label="s(t)")
plt.plot(t, E*(t>=0), label="e(t)")
plt.axhline([0.63*E],c="r", linestyle="--")
plt.axhline([0.95*E],c="r", linestyle="--")
plt.axvline([R*C],c="r", linestyle="--")
plt.axvline([3*R*C],c="r", linestyle="--")
plt.xlim([0, t[-1]])
plt.xlabel("temps [s]")
plt.ylabel("sortie")
plt.legend()
plt.grid()

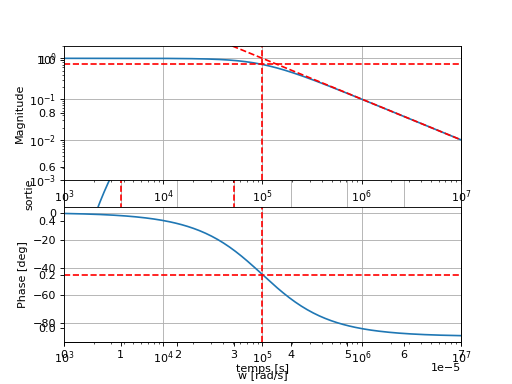
Réponse Fréquentielle#

Expression#

La réponse fréquentielle s’obtient en évaluant la fonction de transfert en \(p=j\omega\). Mathématiquement, nous obtenons :

\[H(j\omega) = \frac{1}{jRC\omega+1}\]

Module :

\[|H(j\omega)| = \frac{1}{\sqrt{(RC\omega)^2+1}}\]

Argument :

\[\arg[H(j\omega)] = -\arctan\left(RC\omega\right)\]

Valeurs Remarquables#

Basse-Fréquence : Lorsque \(\omega\to 0\),

\[\begin{split}|H(j\omega)|&\approx 1,\\ \arg[H(j\omega)]&\approx 0.\end{split}\]

Pulsation de coupure : Lorsque \(\omega=\omega_c=\frac{1}{RC}\),

\[\begin{split}|H(j\omega_c)|&=\frac{1}{\sqrt{2}},\\ \arg[H(j\omega_c)]&=-45^o.\end{split}\]

Asymptotes Haute-Fréquences :

\[\begin{split}\lim_{\omega \to \infty} |H(j\omega)| &= \left(\frac{\omega}{\omega_c}\right)^{-1},\\ \lim_{\omega \to \infty} \arg[H(j\omega)] &= -90^o.\end{split}\]

Simulation Python#

w = np.logspace(3, 7, 200)
wc = 1/(R*C)
w, Hjw = H.freqresp(w=w)
H_mod = np.abs(Hjw)
H_phase = 180*np.angle(Hjw)/np.pi     #convert radian to degree

# plot figure
plt.subplot(2,1,1)
plt.loglog(w,H_mod)
plt.plot([w[0], w[-1]], [wc/w[0], wc/w[-1]],"r--")
plt.axhline([1/np.sqrt(2)],c="r", linestyle="--")
plt.axvline([wc],c="r", linestyle="--")
plt.ylabel("Magnitude")
plt.xlim([w[0], w[-1]])
plt.ylim([0.001, 2])
plt.grid()
plt.subplot(2,1,2)
plt.semilogx(w,H_phase)
plt.axhline([-45],c="r", linestyle="--")
plt.axvline([wc],c="r", linestyle="--")
plt.ylabel("Phase [deg]")
plt.xlabel("w [rad/s]")
plt.xlim([w[0], w[-1]])
plt.grid()