Superposition de courbes en Python#

Dans ce tutorial, nous montrons comment superposer une courbe obtenue avec Scipy et une courbe obtenue analytiquement.

Avant Propos#

Nous allons nous intéresser au module de la réponse fréquentielle d’un système passe-bas de premier ordre. La fonction de transfert d’un passe-bas de premier ordre est donné par

\[H(p)=\frac{T_0}{\frac{1}{\omega_c}p+1}\]

La réponse fréquentielle s’obtient en posant \(p=j\omega\). L’expression analytique du module est alors donnée par:

\[|H(j\omega)|=\frac{T_0}{\sqrt{\left(\frac{\omega}{\omega_c}\right)^2+1}}\]

Implémentation#

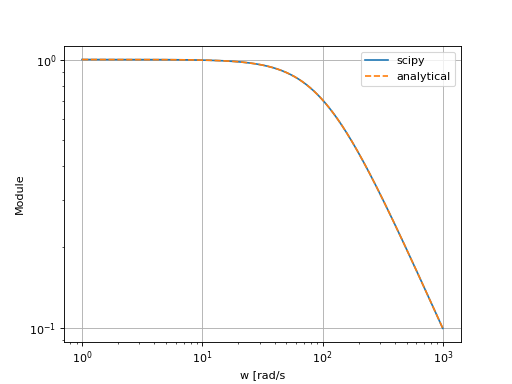
Pour vérifier notre résultat analytique, nous proposons de superposer notre résultat et celui obtenu avec Scipy.

Courbe scipy: le module de la réponse fréquentielle s’obtient en lancant la méthode freqresp. Cette méthode renvoie deux variables: w (un vecteur de pulsation), Hjw (un vecteur contenant la réponse fréquentielle évaluée pour chaque élément de w).
Courbe analytique: la courbe analytique s’obtient en évaluant notre expression analytique pour chaque élément de w.

Pour bien visualiser la superposition de deux courbes identiques, l’implémentation suivante propose d’utiliser le style de ligne -- pour la courbe du dessus.

import numpy as np
import matplotlib.pyplot as plt
from scipy.signal import lti, step

T0 = 1
wc = 100
tau = 1/wc
H = lti([1], [tau, 1])

# frequency response from scipy
w, Hjw = H.freqresp()
H_mod = np.abs(Hjw)

# analytical frequency response
H_mod2 = np.abs(T0) / np.sqrt(1+(w/wc)**2)

# plot figure
plt.loglog(w, H_mod, label="scipy")
plt.loglog(w, H_mod2, "--", label="analytical")
plt.grid()
plt.legend()
plt.xlabel("w [rad/s")
plt.ylabel("Module")