Synthèse des Filtres d’ordre N#

Un filtre est souvent représenté par une fonction de transfert qui détermine comment les différentes fréquences d’un signal d’entrée sont affectées. L’ordre d’un \(N\) d’un filtre est lié à la puissance la plus élevée dans son équation différentielle, ce qui, en retour, est souvent directement lié au nombre de composants nécessaires pour réaliser le filtre.

Plus \(N\) est élevé, plus le filtre est capable d’offrir une transition abrupte entre les fréquences qu’il laisse passer et celles qu’il rejette. Cependant, cela vient aussi avec une complexité accrue et des exigences plus strictes en termes de composants et de conception.

Concevoir un filtre n’est pas simplement une question de choix de l’ordre approprié. La synthèse des filtres concerne la définition des caractéristiques désirées du filtre (comme la bande passante, l’atténuation, la phase) et la conversion de ces spécifications en une conception de circuit ou un algorithme. L’ingénieur doit trouver un compromis entre plusieurs paramètres : rapidité de transition entre les bandes passantes et de coupure, ondulation acceptable dans la bande passante, atténuation minimale dans la bande de coupure, et bien sûr, la complexité et la faisabilité du filtre.

Méthodologie#

  • Étape 1Synthèse du filtre normalisé

    • Définir les spécifications du filtre : Avant toute chose, il est nécessaire de définir les spécifications souhaitées pour le filtre, comme la bande passante, l’atténuation, l’ondulation dans la bande passante, etc. Ces specifications sont précisées via le gabarit fréquentiel.

    • Définir le gabarit du filtre passe-bas normalisé (\(\omega_c=1\) rad/s).

    • Déterminer l’ordre \(N\) du filtre.

    • Synthèse de la fonction de transfert : Avec l’ordre déterminé et la technique de synthèse retenue, utilisez les formules appropriées pour déduire la fonction de transfert \(H_n(p)\) du filtre normalisé.

  • Étape 2Dénormalisation. La dénormalisation consiste à adapter le filtre conçu dans l’étape précédente à vos besoins réels, comme la fréquence de coupure ou la bande passante.

    • Réaliser la substitution \(p\to f(p)\) pour obtenir la fonction de transfert du filtre dénormalisé.

  • Étape 3Réalisation du filtre

    • Sélection des composants : À partir de la fonction de transfert dénormalisée, choisissez des composants (résistances, condensateurs, inductances, etc.) pour réaliser physiquement le filtre.

    • Assemblage et test : Une fois que vous avez tous les composants nécessaires, assemblez le filtre. Testez ensuite ses performances pour vous assurer qu’il répond aux spécifications.

Détermination de l’ordre#

Pour un filtre passe-bas normalisé, il est possible de déterminer l’ordre en utilisant le comportement asymptotique en hautes-fréquences :

\[N = \left\lceil-\frac{\ln\left(\frac{T_c}{T_s}\right)}{\ln\left(\frac{\omega_c}{\omega_s}\right)}\right\rceil\]

  • \(\omega_c=1\) rad/s

  • \(T_c\) correspond à l’amplification minimale dans la bande passante.

  • \(T_s\) correspond à l’amplification maximale dans la bande rejetée.

Dénormalisation#

Pour synthétiser un filtre d’ordre N, la procédure classique consiste à d’abord synthétiser son équivalent “passe-bas” normalisé puis à réaliser une dénormalisation. Soit \(H_n(p)\) la fonction de transfert du filtre normalisé. La fonction du filtre dénormalisé s’obtient en modifiant la variable p de la manière suivante :

\[H(p) = \frac{N(p)}{D(p)}= \left.H_n(p)\right|_{p\to f(p)}\]

  • \(f(p)\): fonction de transformation,

  • \(H_n(p)\): fonction de transfert du filtre normalisé.

Mapping fréquentiel#

Lors de la dénormalisation, la pulsation \(\omega\) est mappé en une ou plusieurs pulsations \(\widehat{\omega}\). Le lien entre \(\omega\) et \(\widehat{\omega}\) est donné par l’équation :

\[\omega = \frac{1}{j}f(j\widehat{\omega})\]

Mapping des pôles et zéros#

Lors de la dénormalisation, le pôle \(p_l\) est mappé en un ou plusieurs pôles \(\widehat{p}_l\). Le lien entre \(p_l\) et \(\widehat{p}_l\) est donné par l’équation :

\[p_l = f(\widehat{p}_l)\]

Note

En pratique, il est plus efficace d’appliquer la dénormalisation directement sur les pôles. Cette stratégie permet de déterminer plus rapidement les pulsations propres \(\omega_0\) et les coefficients d’amortissement \(m\) des différentes cellules d’ordre 2.

Passe-Bas#

Transformation#

\[f(p) = \frac{p}{\omega_c}\]

Mapping Fréquentiel#

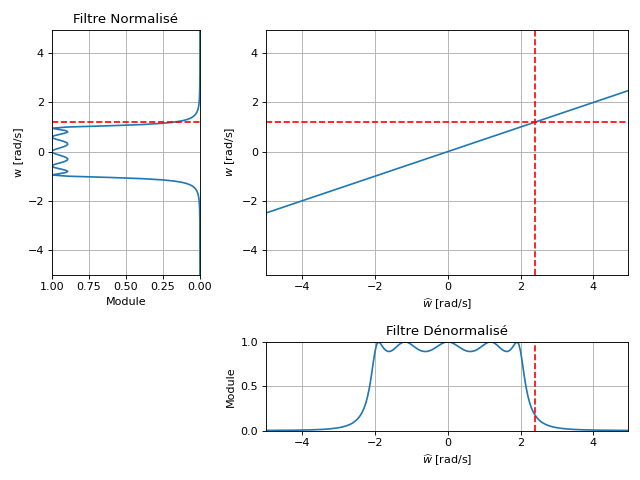
La pulsation \(\omega\) rad/s du filtre normalisé est mappée à la pulsation \(\widehat{\omega}\) telle que

\[j\omega = \frac{j\widehat{\omega}}{\omega_c} \Rightarrow \omega=\frac{\widehat{\omega}}{\omega_c}\]
../_images/filter_synthesis-1.png

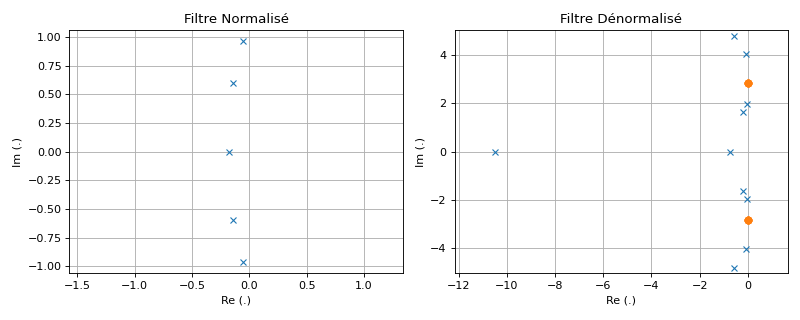
Mapping des pôles et zéros#

Les pôles \(p_l\) et zéros \(z_l\) du filtre normalisé sont mappés aux pôles et zéros

\[\begin{split}\widehat{p}_l&=\omega_c p_l\\ \widehat{z}_l&=\omega_c z_l\end{split}\]
../_images/filter_synthesis-2.png

Passe-Haut#

Transformation#

\[f(p) = \frac{\omega_c}{p}\]

Mapping Fréquentiel#

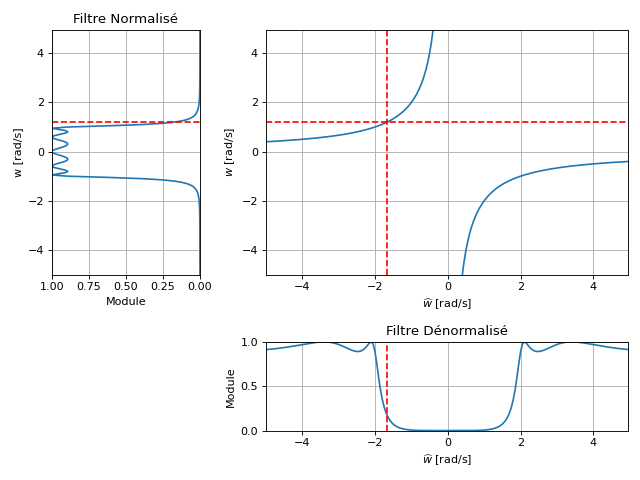
La pulsation \(\omega\) du filtre normalisé est mappée à la pulsation \(\widehat{\omega}\) telle que

\[j\omega = \frac{\omega_c}{j\widehat{\omega}} \Rightarrow \omega =-\frac{\omega_c}{\widehat{\omega}}\]
../_images/filter_synthesis-3.png

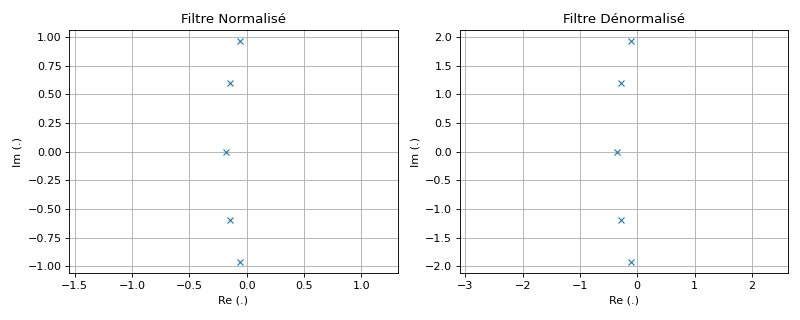
Mapping des pôles et zéros#

Les pôles \(p_l\) et zéros \(z_l\) du filtre normalisé sont mappés aux pôles et zéros

\[\begin{split}\widehat{p}_l&=\omega_c /p_l\\ \widehat{z}_l&=\omega_c /z_l\end{split}\]
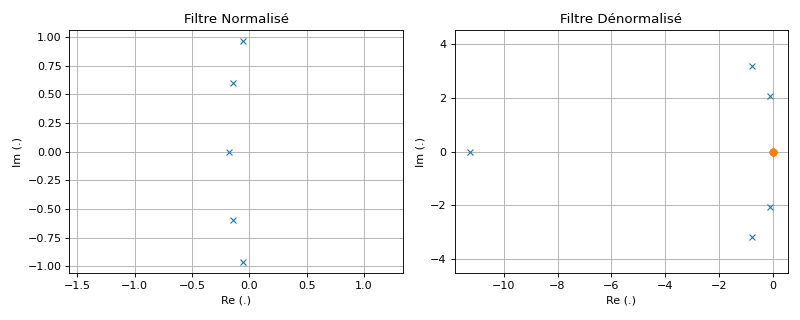
../_images/filter_synthesis-4.png

Passe-Bande#

Transformation#

\[f(p) = \frac{p^2+\omega_0^2}{p\Delta \omega}\]

  • \(\omega_0=\sqrt{\omega_{c1}\omega_{c2}}\) désigne la pulsation centrale,

  • \(\Delta \omega=\omega_{c2}-\omega_{c1}\) désigne la largeur de la bande passante.

Mapping Fréquentiel#

La pulsation \(\omega\) du filtre normalisé est mappée à la pulsation \(\widehat{\omega}\) où

\[j\omega = \frac{(j\widehat{\omega})^2+\omega_0^2}{j\widehat{\omega}\Delta \omega} \Rightarrow \omega = \frac{\widehat{\omega}^2-\omega_0^2}{\widehat{\omega}\Delta \omega}\]
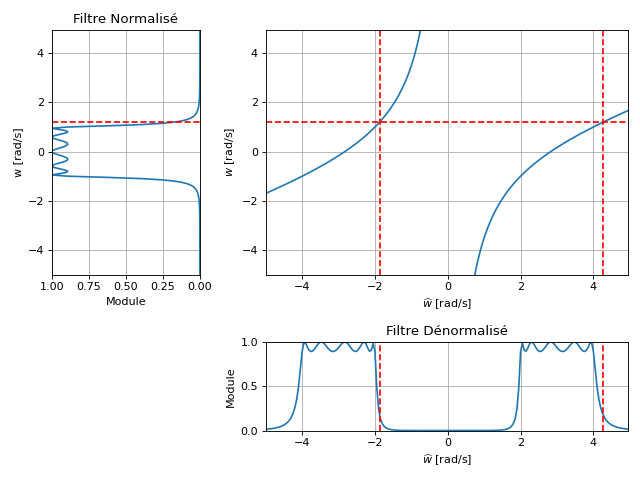
../_images/filter_synthesis-5.png

Mapping des pôles et zéros#

Les pôles \(p_l\) et zéros \(z_l\) du filtre normalisé sont mappés aux pôles et zéros

\[\begin{split}\widehat{p}_l&=\alpha p_l \pm \sqrt{\alpha^2p_l^2-\omega_0^2}\\ \widehat{z}_l&=\alpha z_l \pm \sqrt{\alpha^2z_l^2-\omega_0^2}\end{split}\]

où \(\alpha=\Delta \omega/2\). Pour obtenir un passe-bande, il est également nécessaire d’ajouter plusieurs zéros en 0.

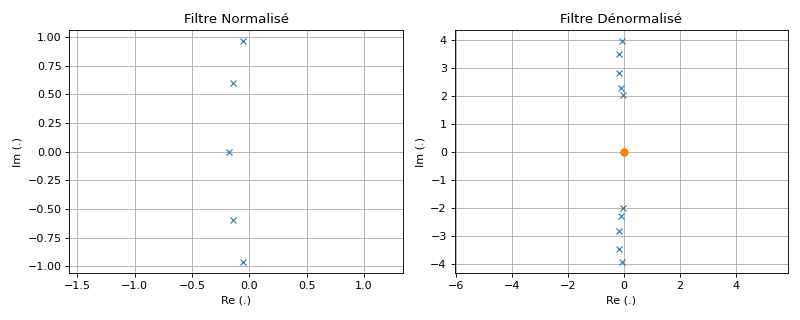
../_images/filter_synthesis-6.png

Rejecteur#

Transformation#

\[f(p) = \frac{p\Delta \omega}{p^2+\omega_0^2}\]

où \(\omega_0=\sqrt{\omega_{c1}\omega_{c2}}\) désigne la pulsation centrale et \(\Delta \omega=\omega_{c2}-\omega_{c1}\) désigne la largeur de la bande passante.

Mapping Fréquentiel#

La pulsation \(\omega\) du filtre normalisé est mappée à la pulsation \(\widehat{\omega}\) où

\[j\omega = \frac{j\widehat{\omega}\Delta \omega}{(j\widehat{\omega}^2)+\omega_0^2} \Rightarrow \omega = \frac{\widehat{\omega}\Delta \omega}{\omega_0^2-\widehat{\omega}^2}\]
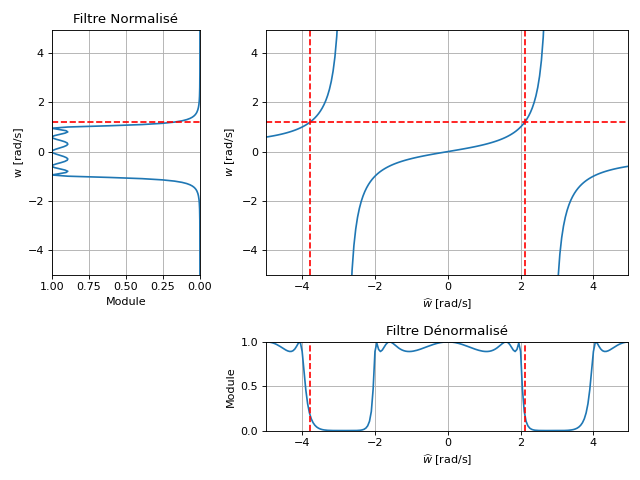
../_images/filter_synthesis-7.png

Mapping des pôles et zéros#

Les pôles \(p_l\) et zéros \(z_l\) du filtre normalisé sont mappés aux pôles et zéros

\[\begin{split}\widehat{p}_l&=\alpha p_l^{-1} \pm \sqrt{\alpha^2p_l^{-2}-\omega_0^2}\\ \widehat{z}_l&=\alpha z_l^{-1} \pm \sqrt{\alpha^2z_l^{-2}-\omega_0^2}\end{split}\]

où \(\alpha=\Delta \omega/2\). Pour obtenir un rejecteur, il est également nécessaire d’ajouter plusieurs zéros en \(\pm j\omega_0\).

../_images/filter_synthesis-8.png