Analyse des systèmes SLIT#

Systèmes SLIT#

Définition#

Un système est dit linéaire s’il obéit au principe de superposition. Cela signifie que la sortie du système à une combinaison linéaire d’entrées est égale à la même combinaison linéaire des sorties individuelles correspondant à ces entrées. Formellement, si un système produit une sortie \(y_1(t)\) en réponse à une entrée \(x_1(t)\) et une sortie \(y_2(t)\) en réponse à \(x_2(t)\), alors pour n’importe quelles constantes \(a\) et \(b\), la sortie due à \(a \times x_1(t) + b \times x_2(t)\) sera \(a \times y_1(t) + b \times y_2(t)\).

L’invariance dans le temps, quant à elle, indique que le comportement du système ne change pas avec le temps. Cela signifie que si une entrée \(x(t)\) produit une sortie \(y(t)\), alors, pour tout retard \(\tau\), l’entrée \(x(t-\tau)\) produira la sortie \(y(t-\tau)\). En d’autres termes, le système répond de la même manière à une même entrée, indépendamment du moment où cette entrée est appliquée.

Un Système Linéaire Invariant dans le Temps, ou SLIT, est un système qui respecte à la fois la propriété de linéarité et celle d’invariance dans le temps. Ces systèmes sont essentiels en ingénierie car ils peuvent être décrits et analysés de manière compacte en utilisant des outils mathématiques tels que la Transformée de Fourier ou la Transformée de Laplace.

Modélisation#

Pour un SLIT, la relation entre l’entrée et la sortie peut être représentée par une équation différentielle linéaire où les coefficients de cette équation ne varient pas avec le temps.

Considérons un système linéaire et invariant dans le temps (SLIT) décrit par une équation différentielle linéaire à coefficients constants d’ordre n :

\[a_n \frac{d^n s(t)}{dt^n} + \cdots+a_1 \frac{d s(t)}{dt} +a_0 s(t) =b_m \frac{d^m e(t)}{dt^m} +\cdots+b_0 e(t)\]

Le plus souvent l’analyse d’un SLIT sera réalisée à partir de la fonction de transfert du système. Au lieu de manipuler des dérivées, l’utilisation de la fonction de transfert permet de revenir à la manipulation de polynômes.

Dans ce cours, nous allons nous focaliser spécifiquement à différent type d’entrées \(e(t)\):

  • Impulsion: Lorsque \(e(t)=\delta(t)\), la sortie du système est appelée réponse impulsionnelle,

  • Echelon d’amplitude E: Lorsque \(e(t)=Eu(t)\), la sortie du système est appelée réponse indicielle,

  • Sinusoïde: Lorsque \(E\cos(\omega t + \varphi_e)\), la sortie du système est appelée réponse fréquentielle.

Fonction de transfert#

La notion de fonction de transfert offre plusieurs avantages par rapport à l’utilisation directe d’équations différentielles lors de l’analyse des systèmes.

  1. Simplification mathématique : Avec la Transformée de Laplace, les équations différentielles se transforment en équations algébriques, qui sont souvent plus simples à manipuler. Par exemple, la dérivation devient une multiplication, ce qui facilite les opérations.

  2. Représentation universelle : La fonction de transfert donne une représentation standard d’un système qui capture ses caractéristiques dynamiques, indépendamment de l’entrée spécifique.

  3. Analyse fréquentielle : La fonction de transfert permet d’analyser facilement le comportement du système en fonction de la fréquence.

  4. Modularité : Lors de la conception de systèmes complexes composés de plusieurs sous-systèmes, chaque sous-système peut être représenté par sa propre fonction de transfert. Ces fonctions de transfert peuvent ensuite être combinées de manière simple (par exemple, par mise en série ou en parallèle) pour obtenir la fonction de transfert du système global.

  5. Facilité d’utilisation avec des outils de simulation : De nombreux outils modernes (comme MATLAB/Simulink ou Python) utilisent la fonction de transfert pour simuler et analyser les systèmes.

Définition#

La fonction de transfert du système est définie par :

\[H(p) = \frac{S(p)}{E(p)}\]

  • \(p \in \mathbb{C}\) désigne la variable de Laplace,

  • \(E(p)=\mathcal{L}[e(t)]\) désigne la transformée de Laplace de l’entrée,

  • \(S(p)=\mathcal{L}[s(t)]\) désigne la transformée de Laplace de la sortie.

L’expression de \(H(p)\) peut s’obtenir

  • à partir de l’équation différentielle en appliquant la transformée de Laplace sous l’hypothèse où les conditions initiales sont nulles,

  • à partir de l’analyse d’un circuit électronique en utilisant directement la notion d’impédance généralisée.

Exemple#

Soit la fonction de transfert de second ordre suivante :

\[a_2 \frac{d^2 s(t)}{dt^2} + a_1 \frac{d s(t)}{dt} +a_0 s(t) = b_0 e(t)\]

En supposant les conditions initiales nulles, nous obtenons dans le domaine de Laplace l’équation algébrique suivante :

\[a_2 p^2S(p) + a_1 pS(p) +a_0 S(p) = b_0 E(p)\]

En factorisant de deux côtés, il en vient que :

\[(a_2 p^2 + a_1 p +a_0) S(p) = b_0 E(p) \Rightarrow H(p)=\frac{b_0}{a_2 p^2 + a_1 p +a_0}\]

La représentation d’une fonction de transfert peut être exprimée sous plusieurs formes, parmi lesquelles les formes canoniques polynomiales, les zéros-pôles-gain (zpk) ou encore les formes d’état.

Forme Polynomiale [ba]#

\[H(p) = \frac{N(p)}{D(p)}=\frac{b_m p^m+\cdots+b_1p+b_0}{a_n p^n+\cdots+a_1 p+a_0}\]

Note

En général, pour un système causal (ce qui est courant en pratique), le degré du numérateur \(m\) ne peut pas être plus élevé que celui du dénominateur \(n\). Nous vérifierons donc systématiquement que \(m\le n\).

Forme Factorisée [zpk]#

Le passage à la forme factorisée s’obtient en évaluant les racines du polynôme au numérateur et les racines du polynôme au dénominateur.

\[H(p) = G\frac{(p-z_m)\times \cdots\times (p-z_1)}{(p-p_n)\times \cdots\times (p-p_1)}\]

  • le paramètre \(G=\frac{b_m}{a_n}\) est un coefficient d’amplification,

  • les zéros \(z_l\) correspondent aux racines du numérateur c-a-d aux solutions de l’équation

\[b_m p^m+\cdots+b_1p+b_0,\]

  • les pôles \(p_l\) correspondent aux racines du dénominateur (c-à-d du polynôme caractéristique) c-a-d aux solutions de l’équation

\[a_n p^n+\cdots+a_1p+a_0 = 0.\]

Il est courant de représenter la localisation des pôles (\(\times\)) et des zéros (\(\circ\)) dans le plan complexes.

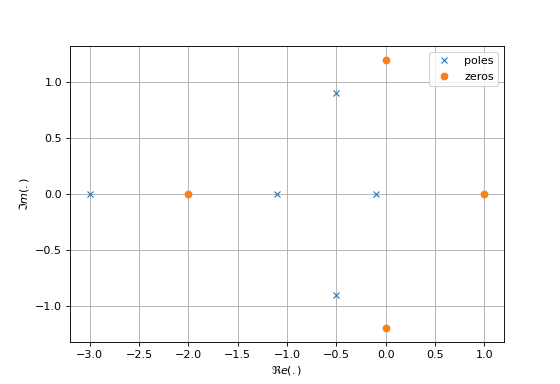
../_images/transfer_function-1.png

La représentation en zéros-pôles-gain (zpk) est particulièrement prisée pour les raisons suivantes :

  • Interprétation physique: Chaque zéro et pôle de la fonction de transfert a une signification physique associée au comportement dynamique du système. Par exemple, un pôle indique une fréquence naturelle du système et peut être lié à des phénomènes tels que la résonance. Cette représentation donne ainsi une vision intuitive du comportement du système.

  • Simplification mathématique: Dans certains cas, il est plus simple et plus direct de travailler avec des zéros et des pôles plutôt qu’avec des polynômes complets, notamment lorsqu’on veut analyser la stabilité d’un système.

  • Multiplication et division: Dans le cadre de la mise en série ou en parallèle de systèmes, il est souvent plus simple de multiplier ou diviser directement les représentations zpk entre elles plutôt que leurs formes polynomiales.

Propriétés#

Stabilité (BIBO)#

Un système est dit stable (au sens BIBO: Bounded Input Bounded Output) si pour toute entrée bornée \(|e(t)|<\infty\), la sortie est également bornée c-à-d \(|s(t)|<\infty\).

Pour qu’un système soit stable, il est possible d’établir que tous les pôles du systèmes doivent posséder une partie réelle négative c-à-d

\[\Re e(p_l)\le 0, \text{ pour }l=1,.., n.\]

Note

Cette propriété découle directement de l’expression générale de la solution libre \(s_l(t)=\sum_{l=1}^{n} \lambda_l e^{p_l t}\).

Gain statique#

Le gain statique est une mesure essentielle pour la conception et l’analyse des systèmes car il donne une première indication sur le comportement d’un système en régime permanent face à des perturbations ou des signaux d’entrée constants.

Le gain statique d’une fonction de transfert, noté \(K\), est défini comme la réponse en régime permanent d’un système à une entrée de type échelon unité, c-à-d \(e(t)=u(t)\), en supposant que le système est initialement au repos (c’est-à-dire, toutes les conditions initiales sont nulles)

Il est possible de determiner le gain statique d’une fonction de transfert \(H(p)\) en posant \(p=0\).

\[K = H(0) = \frac{b_0}{a_0}\]

  • Lorsque l’entrée est une sinusoïde, le gain statique s’obtient en évaluant le gain dans les basse-fréquences c-a-d lorsque \(\omega \to 0\).

  • Si l’entrée et/ou la sortie ne sont pas nulles, le gain statique correspond au rapport entre la variation de la sortie et la variation de l’entrée.

Exemple#

Soit la fonction de transfert de :

\[H(p) = \frac{2p+5}{p^2+3p+2}\]

Le gain statique s’exprime sous la forme :

\[H(0) = \frac{2\times 0+5}{(0)^2+3\times (0) +2}=\frac{5}{2}=2.5\]

A titre d’illustration, si le système est soumis à une entrée en échelon unité, la valeur de sortie en régime permanent sera 2.5 fois la hauteur de cet échelon, soit 2.5.

Comportement Fréquentiel#

Une caractéristique essentielle des systèmes SLIT est que si l’entrée est une sinusoïde de fréquence \(f_0\), la sortie sera aussi une sinusoïde de la même fréquence, mais potentiellement avec une amplitude et une phase modifiées. Le comportement fréquentiel d’un système SLIT permet d’obtenir le gain et le déphasage du signal de sortie en fonction de la fréquence.

Exponentielle Complexe#

Lorsque l’entrée est une exponentielle complexe de pulsation \(\omega\), c-à-d \(e(t)=ce^{j\omega t}\), la sortie est une sinusoïde de même pulsation et s’exprime sous la forme :

\[s(t)=H(j\omega)ce^{j\omega t}.\]

  • \(H(j\omega)\) correspond au gain complexe du système à la pulsation \(\omega\),

Notons que pour tous les systèmes réels (\(a_n\in \mathbb{R}\) et \(b_m\in \mathbb{R}\)), la fonction de transfert \(H(p)\) respectera la propriété de symétrie hermitienne suivante: \(H(p) = H^*(-j\omega)\).

Sinusoïde#

Lorsque l’entrée est une sinusoïde de pulsation \(\omega\), c-à-d \(e(t)=E\cos(\omega t + \varphi_e)\), la sortie est une sinusoïde de même pulsation et s’exprime sous la forme :

\[s(t)=|H(j\omega)|E\cos(\omega t + \varphi_e + \arg[H(j\omega)]),\]

  • \(|H(j\omega)|\) correspond au gain du système à la pulsation \(\omega\),

  • \(\arg[H(j\omega)]\) correspond au déphasage du système à la pulsation \(\omega\).

L’allure du gain \(|H(j\omega)|\) permet de caractériser le type de filtre (passe-bas, passe-bande, passe-haut, rejecteur, …)