Systèmes de Premier Ordre#

Modélisation#

Equation différentielle#

\[\tau\frac{d s(t)}{dt} + s(t) = b_1\frac{d e(t)}{dt}+e(t)\]

  • \(\tau\) désigne la constante de temps [s].

Fonction de transfert#

La fonction de transfert d’un système de premier ordre peut s’exprimer sous la forme normalisée suivante :

\[H(p)=\frac{N(p)}{\frac{1}{\omega_c}p+1}\]

  • \(N(p)\) désigne le numérateur de la fonction de transfert (polynôme de degré inférieur ou égale à 1).

  • \(\omega_c=\frac{1}{\tau}\) désigne la pulsation de coupure à -3dB [rad/s].

Expression du pôle#

Un système de premier ordre possède un unique pôle. Ce pôle s’obtient en cherchant l’unique racine du dénominateur de la fonction de transfert.

\[\tau p+1 = 0 \Rightarrow p = -\frac{1}{\tau} = -\omega_c\]

Exemples#

\[\begin{split}H_{LP}(p)&=\frac{T_0}{\frac{1}{\omega_c}p+1}\\ H_{HP}(p)&=\frac{\frac{T_\infty}{\omega_0}p}{\frac{1}{\omega_c}p+1}\end{split}\]

Réponse Temporelle#

La solution complète de l’équation différentielle s’exprime sous la forme :

\[s(t)=s_l(t)+s_p(t)\]

  • \(s_l(t)\): solution libre (régime libre)

\[s_l(t)=\lambda e^{-\frac{1}{\tau} t}\]

  • \(s_p(t)\): solution particulière (régime forcé). L’expression du régime forcé dépend de l’allure de l’entrée et des coefficients \(b_1\) et \(b_2\)

Exemple (LP)#

Considérons la réponse d’un système de premier ordre a un échelon d’amplitude \(E\), c-à-d \(e(t)=Eu(t)\). Le système est supposé initialement au repos (\(s(0^-)=0\)). Comme l’entrée est un échelon, le regime forcé est de la forme \(s_p(t)=Su(t)\). En remplaçant cette expression dans l’équation différentielle pour \(t\ge 0\), nous obtenons \(s_p(t)=T_0E\). Il en vient que :

\[s(t)=\lambda e^{-\frac{1}{\tau} t}+T_0E\]

La constante d’intégration s’obtient en déterminant une condition initiale. En intégrant l’équation différentielle entre \(t=0^-\) et \(t=0^+\), nous obtenons \(s(0^+) = 0\) En exploitant cette equation, il en vient que :

\[s(0^+) =\lambda \times 1 + T_0E = 0 \Rightarrow \lambda = -T_0 E,\]

Pour un filtre passe-bas de premier ordre, la réponse du système a un échelon d’amplitude \(E\) s’exprime finalement sous la forme :

\[s(t) = T_0 E\left(1-e^{-\frac{1}{\tau} t}\right)\]

Valeurs Remarquables#

  • Valeur initiale : \(s(0^+)=0\),

  • Valeur finale : \(s(\infty)=T_0 E\),

  • Valeur maximale: \(\max(s(t))=T_0 E\),

  • Temps de réponse à \(\pm 5\%\): \(t_r=3\tau\).

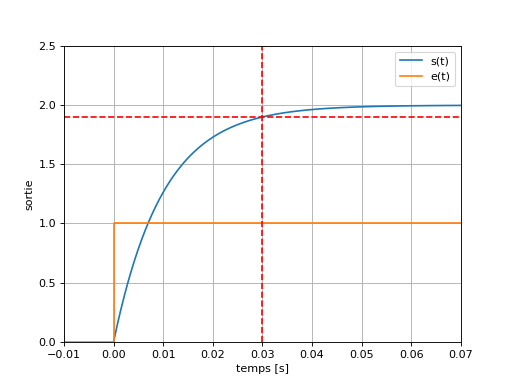
../_images/first_order-1.png

Réponse Fréquentielle#

La réponse fréquentielle s’obtient en posant \(p=j\omega\) dans l’expression de la fonction de transfert. Nous obtenons :

\[H(j\omega)=\frac{N(j\omega)}{j\frac{\omega}{\omega_c}+1}\]

Passe-Bas#

  • Module :

\[|H(j\omega)|=\frac{T_0}{\sqrt{\left(\frac{\omega}{\omega_c}\right)^2+1}}\]

  • Argument :

\[\arg[H(j\omega)]=-\arctan\left( \frac{\omega}{\omega_c} \right)\]
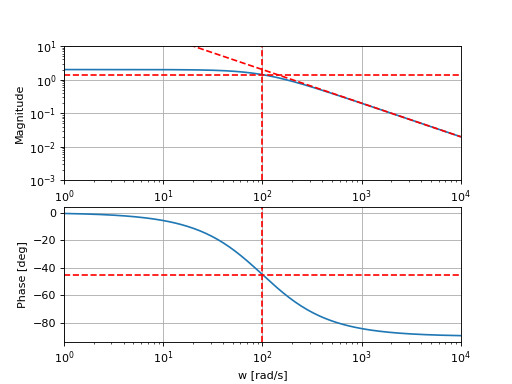
../_images/first_order-2.png

Passe-Haut#

  • Module :

\[|H(j\omega)|=\frac{T_\infty\frac{\omega}{\omega_c}}{\sqrt{\left(\frac{\omega}{\omega_c}\right)^2+1}}\]

  • Argument :

\[\arg[H(j\omega)]=90^o-\arctan\left( \frac{\omega}{\omega_c} \right)\]
../_images/first_order-3.png