Rappels Mathematiques#

Nombres Complexes#

Notons \(j\) l’imaginaire pur tel que \(j^2=-1\) et \(\mathbb{C}\) le corps des complexes.

Forme algébrique#

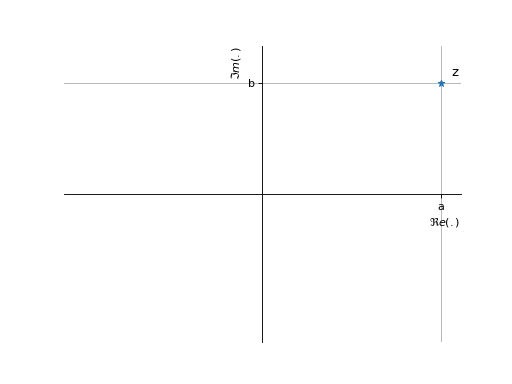
Tout nombre complexe \(z\in \mathbb{C}\) s’écrit sous la forme :

\[z=a+jb\]

  • \(a=\Re e(z)\) correspond à la partie réelle,

  • \(b=\Im m(z)\) correspond à la partie imaginaire.

../../_images/math-1.png

Complexe Conjugué#

On appelle conjugué de \(z\) le nombre complexe

\[z^*=a-jb\]

Exponentielle Complexe#

L’exponentielle complexe est définie par

\[e^{j\theta}=\cos(\theta)+j\sin(\theta)\]

  • Multiplication : La multiplication de deux exponentielles complexes donne : \(e^{j\theta_1}e^{j\theta_2}=e^{j(\theta_1+\theta_2)}\),

  • Conjugaison : Le conjugué d’une exponentielle complexe est égal à : \(\left(e^{j\theta}\right)^*=e^{-j\theta}\),

  • Périodicité: L’exponentielle complexe est \(2\pi\)-périodique,

  • Formules d’Euler : Les formules d’Euler permettent d’exprimer le cosinus ou le sinus à partie de l’exponentielle complexe

\[\begin{split}\cos(\theta)=\Re e(e^{j\theta})=\frac{1}{2}\left(e^{j\theta}+e^{-j\theta}\right)\\ \sin(\theta)=\Im m(e^{j\theta})=\frac{1}{2j}\left(e^{j\theta}-e^{-j\theta}\right)\end{split}\]

Forme Polaire#

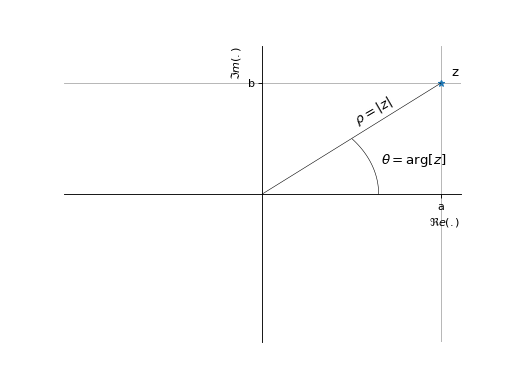
Tout nombre complexe \(z\in \mathbb{C}\) non nul peut s’écrire sous la forme :

\[z=\rho e^{j\theta}\]

  • \(\rho = |z|\) correspond au module,

  • \(\theta=\arg[z]\) correspond à l’argument (modulo \(2\pi\)).

../../_images/math-2.png

Propriétés#

Soit deux complexes \(z_1\) et \(z_2\).

  • Le module et l’argument de \(z=z_1z_2\) sont donnés par :

\[\begin{split}|z|&=|z_1| \times |z_2|\\ \arg[z] &= \arg[z_1]+\arg[z_2]\end{split}\]

  • Le module et l’argument de \(z=z_1/ z_2\) sont donnés par :

\[\begin{split}|z|&=\frac{|z_1|}{|z_2|}\\ \arg[z] &= \arg[z_1]-\arg[z_2]\end{split}\]

Conversion#

Soit un nombre complexe \(z=a+jb\), alors

\[\begin{split}|z|&=\sqrt{a^2+b^2}\\ \theta&= \left\{\begin{array}{lc} \arctan(b/a) & \text{, si }a>0,\\ \pi +\arctan(b/a) & \text{, si }a<0.\\ \end{array}\right.\end{split}\]

Polynômes#

Forme générale#

Modèle Mathématique#

Un polynôme de degré \(n\) est décrit par l’équation suivante :

\[p(x)=a_nx^n+\cdots + a_1 x+a_0\]

  • \(n\) correspond au degré du polynôme,

  • \(a_l\) correspondent aux coefficients du polynôme.

Racines#

Les racines d’un polynôme de degré \(n\) correspondent aux solutions de l’équation polynomiale suivante :

\[p(x)=0\]

Lorsque les coefficients \(a_l\) sont réels et non nuls, le polynôme \(p(x)\) possède au plus \(n\) racines. Ces racines peuvent être réelles ou complexes.

Cas du degré 2#

Modèle Mathématique#

Un polynôme de degré 2 est décrit par l’équation suivante :

\[p(x)=a x^2+ b x+c\]

Racines#

L’expression des racines s’obtient en évaluant le discriminant :

\[\Delta = b^2 - 4ac\]

  • Si \(\Delta>0\), le polynôme possède deux racines réelles distinctes :

\[\begin{split}x_1 = \frac{-b+\sqrt{\Delta}}{2a}\\ x_2 = \frac{-b-\sqrt{\Delta}}{2a}\end{split}\]

  • Si \(\Delta=0\), le polynôme possède une racine double réelle :

\[x_1 = x_2 = -\frac{b}{2a}\]

  • Si \(\Delta<0\), le polynôme possède deux racines complexes distinctes :

\[\begin{split}x_1 = \frac{-b+j\sqrt{-\Delta}}{2a}\\ x_2 = \frac{-b-j\sqrt{-\Delta}}{2a}\end{split}\]