Synthèse de Filtres#

Filtre FIR#

Synthèse par Fenêtrage#

Considérons le cas où nous souhaitons synthétiser un filtre FIR d’ordre N à phase linéaire dont la réponse fréquentielle est donnée par

\[H_d(e^{j\omega})=|H_d(e^{j\omega})|e^{-j\omega N/2}\]

Pour obtenir les coefficient du filtre FIR, nous allons procéder de la manière suivante :

  1. Calcul de la réponse impulsionnelle théorique \(h_d[n]\),

  2. Troncature temporelle de la réponse impulsionnelle,

  3. [optionnel] Application d’une fenêtre de pondération temporelle pour limiter l’effet de la troncature temporelle.

Exemple#

Cahier des charges#

Pour illustrer cette partie, nous allons synthétiser un filtre d’ordre N dont le module de la réponse fréquentielle est donné par :

\[\begin{split}|H_d(e^{j\omega})|&=\left\{\begin{array}{cl} 1&\textrm{, pour } |\omega| \le \omega_c\\ 0 &\textrm{, ailleurs}\end{array}\right.\end{split}\]

  • \(\omega_c\) désigne la pulsation de coupure normalisée (\(\omega_c = 2\pi(f_c/f_s)\) où \(f_c\) désigne la fréquence de coupure [Hz] et \(f_s\) désigne la fréquence d’échantillonnage [Hz]).

Ce filtre est un filtre passe-bas en mur de briques (pente infinie). En imposant une phase linéaire, la réponse fréquentielle de ce filtre est donnée par

\[H_d(e^{j\omega})=|H_d(e^{j\omega})|e^{-j\omega N/2}\]

Réponse Impulsionnelle#

La réponse impulsionnelle du filtre s’obtient en utilisant l’expression :

\[h_d[n]= \frac{1}{2\pi}\int_{-\pi}^{\pi} H(e^{j\omega})e^{j\omega n}d\omega\]

Après quelques calculs, nous obtenons :

\[h_d[n] =\frac{\sin\left(\omega_c (n-N/2)\right)}{\pi (n-N/2)}\]

Pour obtenir un filtre d’ordre N, nous allons conserver uniquement les (N+1) premiers échantillons de la réponse impulsionnelle. La réponse impulsionnelle utilisée s’exprime alors sous la forme :

\[h[n] = w[n]h_d[n]\]

où \(w[n]\) est une fenêtre de pondération telle que \(w[n]=0\) si \(n<0\) ou \(n> N\).

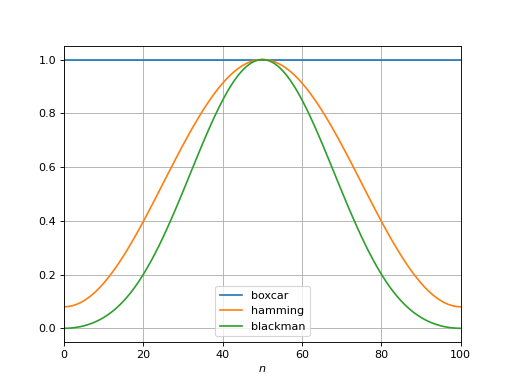
Fenêtres de pondération#

Nom

Fonction scipy

\(w[n]\)

Rectangulaire

boxcar

\(1\)

Hamming

hamming

\(0.54 - 0.46 cos\left(\frac{2\pi n}{N-1}\right)\)

Blackman

blackman

\(0.42 - 0.5 cos\left(\frac{2\pi n}{N}\right)+ 0.08 cos\left(\frac{4\pi n}{N}\right)\)

 
from scipy.signal import get_window
import matplotlib.pyplot as plt

N = 100
window_name_list = ["boxcar", "hamming", "blackman"]

for window_name in window_name_list:
    w = get_window(window_name, N+1, fftbins=False)
    plt.plot(w, label=window_name)

plt.grid()
plt.xlim([0, N])
plt.xlabel("$n$")
plt.legend()
../../_images/design-1.png

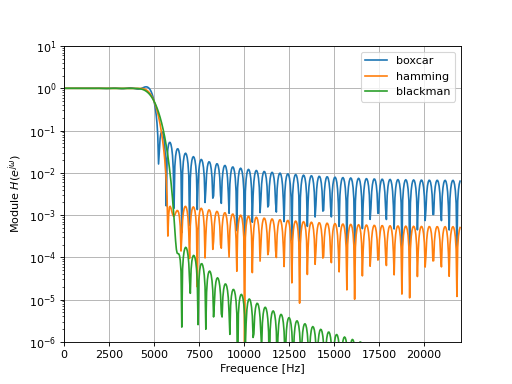
Réponse fréquentielle#

La figure suivante présente l’allure de la réponse fréquentielle obtenue avec les paramètres suivants :

  • ordre: \(N=101\)

  • pulsation de coupure : \(\omega_c=f_c/F_e\) avec \(f_c=5000`Hz et :math:`f_e=44100\) Hz,

  • fenêtre de pondération: boxcar ou hamming ou blackman.

Le script suivant présente l’allure des réponses fréquentielles. Notons que la fenêtre rectangulaire (boxcar) ne permet pas d’obtenir une attenuation importante dans la bande rejetée à cause de la présence de lobes importants.

import numpy as np
from scipy.signal import freqz, get_window
import matplotlib.pyplot as plt

N = 100
f_c = 5000
fs = 44100

w_c = 2*np.pi*(f_c/fs)
window_name_list = ["boxcar", "hamming", "blackman"]

n_vect = np.arange(N+1)
# be careful to the definition of the sinc function (see documentation)
h_d = (w_c/np.pi)*np.sinc((w_c/np.pi)*(n_vect-int((N+1)/2)))

for window_name in window_name_list:
    w = get_window(window_name, N+1, fftbins=False)
    h = w*h_d
    f, Hjw = freqz(h, fs=fs)
    plt.semilogy(f, np.abs(Hjw), label=window_name)

plt.ylabel("Module $H(e^{j\omega})$")
plt.xlabel("Frequence [Hz]")
plt.xlim([0, fs/2])
plt.ylim([10**-6, 10])
plt.grid()
plt.legend()
../../_images/design-2.png

Filtre IIR#

Pour concevoir un filtre numérique IIR, une technique possible consiste à convertir un filtre analogique. En utilisant cette approche, nous allons pouvoir réutiliser un large panel de techniques initialement développées dans le contexte analogique. Dans le domaine analogique, un filtre est décrit par sa fonction de transfert, \(H_a(s)\), où \(s\) désigne la variable de Laplace.

Dans les sous-sections suivantes, nous allons présenter deux techniques permettant d’approcher la réponse fréquentielle d’un filtre analogique par un filtre numérique.

Invariance Impulsionnelle#

Principe#

La technique de synthèse basée sur l’invariance impulsionnelle est décrite par la procédure suivante

  1. Décomposition en éléments simples de la fonction de transfert \(H_a(s)\),

  2. Calcul de la réponse impulsionnelle à temps continu: \(h_a(t)=\mathcal{L}^{-1}\{H_a(s)\}\) où \(\mathcal{L}^{-1}\{.\}`\) désigne la transformée de Laplace inverse.

  3. Discrétisation de la réponse impulsionnelle: \(h[n]=T_s h_a(n T_s)\), où \(T_s\) désigne la période d’échantillonnage.

  4. Détermination de la fonction de transfert en \(\mathcal{Z}\), \(H(z)=\mathcal{Z}\{h[n]\}\) via le tableau des transformées en Z.

  5. Obtention de l’équation aux différences à partir de \(H(z)\)

Propriété#

Lorsque la fonction de transfert \(H_a(s)\) contient uniquement des pôles de premier ordre et se décompose sous la forme :

\[H_a(s)=\sum_{k=1}^{N} \frac{A_k}{s-p_k},\]

la fonction de transfert \(H(z)\) est simplement égale à

\[H(z)=\sum_{k=1}^{N} \frac{T_s A_k}{1-e^{p_kT_e}z^{-1}}\]

Cette expression montre que la synthèse du filtre s’obtient :

  • en réalisant le mapping des pôles \(p_k\to e^{p_kT_s}\),

  • en multipliant le numérateur par le coefficient \(T_s\).

Transformée Bilinéaire#

Dans le domaine analogique, un filtre est décrit par une équation différentielle. Pour numériser un filtre analogique, une approche possible consiste à utiliser une technique d’intégration numérique basée sur la méthode des trapèzes. Cette approche est nommée transformée bilinéaire. En pratique, la transformée bilinéaire s’obtient simplement en réalisant la substitution :

\[s \to \frac{2}{T_s}\frac{1-z^{-1}}{1+z^{-1}}\]

  • \(T_s=\frac{1}{f_s}\): période d’échantillonnage.

Propriétés#

  • Un point appartenant à l’axe \(s=j\omega\) dans le plan de Laplace est déplacé en un point appartenant au cercle de rayon unité \(e^{j\omega}\) dans le domaine en \(\mathcal{Z}\).

  • Après transformation, la pulsation \(\omega_a\) dans le domaine continue est déplacée à la pulsation \(\omega_c\) dans le domaine numérique. Le lien entre ces deux pulsations est donné par

\[\omega_a=\frac{2}{T_s}\tan\left(\omega_c\frac{T_s}{2}\right)\]

Principe#

L’utilisation de la transformée bilinéaire introduit une distorsion non-linéaire de l’axe fréquentiel. Pour limiter cette distorsion, nous allons imposer que la réponse fréquentielle du filtre numérique soit la même que celle du filtre analogique à la pulsation \(\omega_c\). En imposant cette contrainte, nous obtenons la méthodologie suivante :

  1. Prewarping de la fréquence de coupure \(\omega_c\) :

\[\omega_a = \frac{2}{T_s}\tan\left( \frac{T_s\omega_c}{2}\right)\]

  1. Synthèse du filtre analogique \(H_a(s)\) en utilisant la pulsation de coupure \(\omega_a\),

  2. Application de la transformée bilinéaire

\[H(z) = H_a\left(\frac{2}{T_s}\frac{1-z^{-1}}{1+z^{-1}}\right)\]

Exemple#

Cahier des charges#

Pour illustrer l’utilisation des deux techniques de synthèse, nous allons considérer le cas d’un filtre de Butterworth analogique d’ordre 2 et de pulsation de coupure \(f_c\). La fonction de transfert est alors donnée par:

\[H_a(s)=\frac{\omega_c^2}{(s-\omega_c e^{3j\pi/4})(s-\omega_c e^{-3j\pi/4})}=\frac{\omega_c^2}{s^2+\omega_c\sqrt{2}s+\omega_c^2}\]

Dans notre exemple, nous allons prendre \(\omega_c = 2\pi (5000)=31415.926\) [rad/s] et \(T_s= 1/44100\) [s].

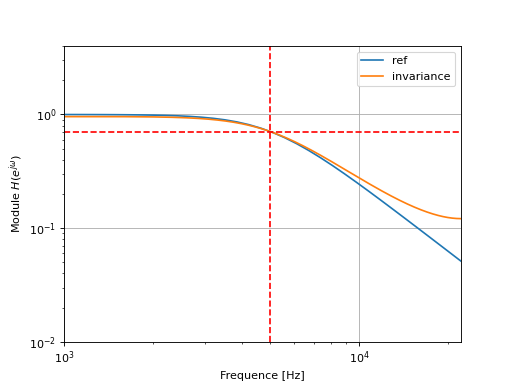
Invariance Impulsionnelle#

La fonction de transfert peut se décomposer sous la forme :

\[H_a(s)=\frac{A_1}{s-p_1} + \frac{A_2}{s-p_2}\]

  • \(A_1=-j\frac{\omega_c}{\sqrt{2}}=-A_2\)

  • \(p_1=\omega_c e^{3j\pi/4}=p_2^*\).

La fonction de transfert discrète du filtre IIR est donc égale à :

\[H(z)=A_1T_s\left(\frac{1}{1-e^{p_1T_s}z^{-1}} - \frac{1}{1-e^{p_1^*T_s}z^{-1}}\right)\]

En utilisant les valeurs numériques et en ramenant tout sous le même dénominateur, nous obtenons :

\[H(z)=\frac{-0.2938z^{-1}}{1-1.0584z^{-1}+0.3651z^{-2}}\]

La figure suivante présente la réponse fréquentielle du filtre synthétisé. Nous pouvons remarquer la présence d’artefacts à proximité de la fréquence de Shannon \(f_s/2\) (repliement spectral).

import numpy as np
from scipy.signal import butter, lti, dlti
import matplotlib.pyplot as plt

f_c = 5000
fs = 44100

# construct analog butterworth filter
b, a = butter(2, 2*np.pi*f_c, 'low', analog=True)
Ha = lti(b,a)
w, Hajw = Ha.freqresp(w=np.logspace(2, 6, 100))
f = w/(2*np.pi)
plt.loglog(f, np.abs(Hajw), label="ref")

# discrete filter using invariance method
H = dlti([0, -0.2938, 0], [1, -1.0584, 0.3651])
w, Hjw = H.freqresp()
f = fs*w/(2*np.pi)
plt.loglog(f, np.abs(Hjw), label="invariance")

plt.axhline(1/np.sqrt(2),c='r', linestyle="--")
plt.axvline(f_c,c='r', linestyle="--")
plt.ylabel("Module $H(e^{j\omega})$")
plt.xlabel("Frequence [Hz]")
plt.xlim([10**3, fs/2])
plt.ylim([10**-2, 4])
plt.grid()
plt.legend()
../../_images/design-3.png

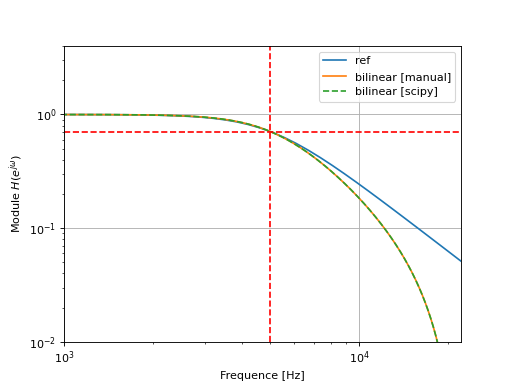
Transformée Bilinéaire#

En appliquant un prewarping de la fréquence de coupure \(\omega_c\), nous obtenons

\[\omega_a = \frac{2}{T_s}\tan\left( \frac{T_s\omega_c}{2}\right) = 32815.59 [rad/s]\]

Après transformation, la fonction de transfert du filtre peut s’exprimer sous la forme :

\[H(z) = \frac{\Omega^2 (1+2z^{-1}+z^{-2})}{(\Omega^2+2\Omega \sqrt{2}+4)+2(\Omega^2-4)z^{-1}+(\Omega^2-2\Omega \sqrt{2}+4)z^{-2}}\]

  • où \(\Omega=\omega_a T_s\) désigne la pulsation normalisée.

import numpy as np
from scipy.signal import butter, lti, dlti
import matplotlib.pyplot as plt

f_c = 5000
fs = 44100
Ts = 1/fs

# construct analog butterworth filter
b, a = butter(2, 2*np.pi*f_c, 'low', analog=True)
Ha = lti(b,a)
w, Hajw = Ha.freqresp(w=np.logspace(2, 6, 100))
plt.loglog(w/(2*np.pi), np.abs(Hajw), label="ref")

# discrete filter using bilinear transform
# prewarping
w_c = 2*np.pi*f_c
w_a = (2/Ts)*np.tan(Ts*w_c/2)
Omega = w_a*Ts
# apply bilinear transform
b_1 = [Omega**2, 2*Omega**2 , Omega**2]
a_1 = [Omega**2 + 2*Omega*np.sqrt(2) + 4, 2*(Omega**2 - 4), Omega**2 - 2*Omega*np.sqrt(2) + 4]
H_1 = dlti(b_1, a_1)
w, H_1jw = H_1.freqresp()
plt.loglog(fs*w/(2*np.pi), np.abs(H_1jw), label="bilinear [manual]")

# scipy function to make the job directly
b_2, a_2 = butter(2, w_c/(2*np.pi), 'low', analog=False, fs=fs)
H_2 = dlti(b_2, a_2)
w, H_2jw = H_2.freqresp()
plt.loglog(fs*w/(2*np.pi), np.abs(H_2jw), linestyle="--", label="bilinear [scipy]")

plt.axhline(1/np.sqrt(2),c='r', linestyle="--")
plt.axvline(f_c,c='r', linestyle="--")
plt.ylabel("Module $H(e^{j\omega})$")
plt.xlabel("Frequence [Hz]")
plt.xlim([10**3, fs/2])
plt.ylim([10**-2, 4])
plt.grid()
plt.legend()
../../_images/design-4.png