Analyse de Filtres#
Une grande partie des filtres LTI peut être modélisée par une équation de récurrence :
Dans cette section, nous allons introduire des outils pour comprendre comment la valeur des coefficients \(b_m\) et \(a_l\) impacte la sortie du filtre.
Transformée en Z#
Définition#
La transformée en \(\mathcal{Z}\) d’une suite numérique \(x[n]`\) est définie par l’équation
\(z\) est une variable complexe.
Il est important de noter que la transformée de Z d’un signal ne converge pas nécessairement pour toutes les valeurs \(z \in \mathbb{Z}\). Il est alors nécessaire de préciser la région de convergence (ROC) pour laquelle la série converge c-à-d les valeurs de \(z\) telles que \(|X(z)|<\infty\).
Tables des transformées#
A titre d’illustration, le tableau suivant présente les transformées en Z de plusieurs signaux et leurs regions de convergence associées.
Signal |
Transformée en Z |
ROC |
|---|---|---|
\(\delta[n]\) |
\(1\) |
\(z \in \mathbb{Z}\) |
\(u[n]\) |
\(\frac{1}{1-z^{-1}}\) |
\(|z| > 1\) |
\(\delta[n-m]\) |
\(z^{-m}\) |
\(z \ne 0\) |
\(à^n u[n]\) |
\(\frac{1}{1-az^{-1}}\) |
\(|z| > |à|\) |
\(na^n u[n]\) |
\(\frac{az^{-1}}{(1-az^{-1})^2}\) |
\(|z| > |à|\) |
\(\cos (\omega_0 n)u[n]\) |
\(\frac{1-\cos(\omega_0)z^{-1}}{1-2\cos(\omega_0)z^{-1}+z^{-2}}\) |
\(|z| > 1\) |
\(\sin (\omega_0 n)u[n]\) |
\(\frac{\sin(\omega_0)z^{-1}}{1-2\cos(\omega_0)z^{-1}+z^{-2}}\) |
\(|z| > 1\) |
\(r^n\cos (\omega_0 n)u[n]\) |
\(\frac{1-r\cos(\omega_0)z^{-1}}{1-2r\cos(\omega_0)z^{-1}+r^2z^{-2}}\) |
\(|z| > r\) |
\(r^n\sin (\omega_0 n)u[n]\) |
\(\frac{r\sin(\omega_0)z^{-1}}{1-2r\cos(\omega_0)z^{-1}+r^2z^{-2}}\) |
\(|z| > r\) |
Propriétés#
La transformée en Z possède les propriétés suivantes :
Linéarité: Si \(y[n]=\alpha x_1[n]+\beta x_2[n]\), alors \(Y(z)=\alpha X_1(z)+\beta X_2(z)\).
Décalage temporel: Si \(y[n]=x[n-m]\) (\(m \in \mathbb{Z}\)), alors \(Y(z)=X(z)z^{-m}\).
Multiplication par une fonction exponentielle: Si \(y[n]= à^n x[n]\), alors \(Y(z)=X(z/à)\).
Convolution: Si \(y[n]= h[n]*x[n]\), alors \(Y(z)=H(z)X(z)\).
Théorème de la valeur finale: \(\lim_{n\to \infty} x[n]=\lim_{z\to 1}(z-1)X(z)\).
Fonction de transfert#
La fonction de transfert d’un filtre correspond à la transformée en Z de sa réponse impulsionnelle c-à-d
\(h[n]=T\{\delta[n]\}\) correspond à la réponse impulsionnelle du filtre.
La propriété liée à la convolution montre que la fonction de transfert d’un filtre peut également s’exprimer sous la forme
\(X(z)\): transformée en Z de l’entrée,
\(Y(z)\): transformée en Z de la sortie.
Pour un filtre décrit par une équation de récurrence, cette propriété permet d’exprimer facilement la fonction de transfert du filtre en fonction des coefficients des parties récursive \(a_l\) et non-recursive \(b_m`\) du filtre.
Forme polynomiale#
La fonction de transfert d’un filtre numérique décrit par une équation de récurrence s’exprime sous la forme:
\(a_0 = 1\) (forme normalisée)
Exemple#
Considérons le filtre décrit par l’équation de récurrence suivante :
Il est possible de montrer que la fonction de transfert de ce filtre est donnée par
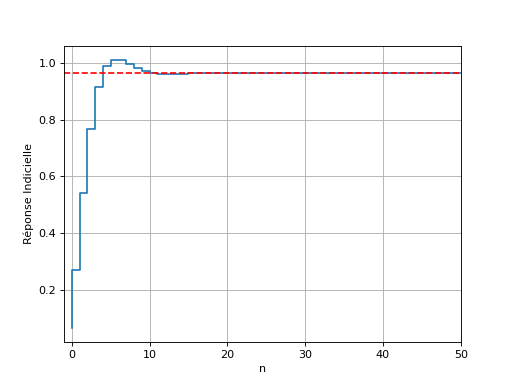
La transformée en Z de la sortie s’obtient en évaluant \(Y(z)=H(z)X(z)\). A titre d’exemple, si l’entrée du filtre est un échelon unitaire (réponse indicielle), la transformée en Z de la sortie sera égale à \(Y(z)=H(z)/(1-z^{-1})\). En utilisant le théorème de la valeur finale, nous pouvons alors anticiper qu’en temporel la valeur finale sera égale à \(\lim_{n\to\infty}y[n]=H(1)=0.962\). Pour confirmer ce résultat, la figure suivante présente la réponse du filtre lorsqu’un échelon unitaire est envoyé en entrée. Nous pouvons constater que la valeur finale est bien égale à \(0.962\).
from scipy.signal import dlti
import matplotlib.pyplot as plt
num = [0.065, 0.13, 0.065]
den = [1, -1.143, 0.413]
H = dlti(num, den)
n, y = H.step()
# affichage de la reponse indicielle
plt.step(n, np.squeeze(y))
plt.axhline(y=0.962, color="r", linestyle="--")
plt.grid()
plt.xlabel("n")
plt.ylabel("Réponse Indicielle")
plt.xlim([-1, 50])
Forme factorisée#
Pour mettre en évidence les comportements singuliers de la fonction de transfert pour différentes valeurs de \(z\), il est possible de réexprimer la fonction de transfert sous une forme factorisée.
La forme factorisée présente explicitement les valeurs de \(z\) pour lesquelles \(H(z)\) tend vers 0 (zéros) et les valeurs de \(z\) pour lesquelles \(H(z)\) tend vers l’infini (pôles).
\(G\) est un facteur de gain,
les valeurs \(z_m\) correspondent respectivement aux zéros de la fonction de transfert,
les valeurs \(p_l\) correspondent respectivement aux pôles de la fonction de transfert.
Notons que comme les coefficients \(a_l\) et \(b_m\) sont réels, les pôles et zéros complexes sont nécessairement réels ou complexe-conjugués.
Répresentation#
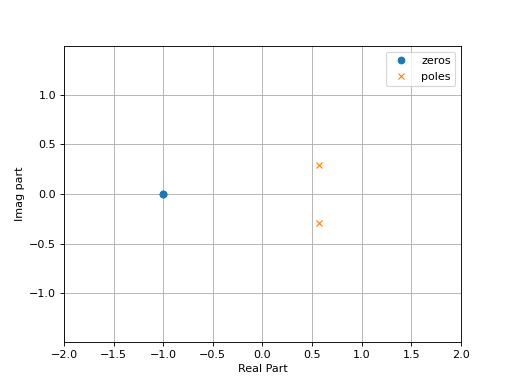
Il est courant de représenter la localisation des pôles et des zéros dans le plan complexe. Par convention, les pôles sont indiqués avec un \(\times\) et les zéros avec un \(\circ\). La figure suivante présente la localisation des pôles et des zéros pour le filtre 1.
from scipy.signal import dlti
import matplotlib.pyplot as plt
num = [0.065, 0.13, 0.065]
den = [1, -1.143, 0.413]
H = dlti(num, den)
poles = H.poles
zeros = H.zeros
# affichage des poles et zeros
plt.plot(np.real(zeros), np.imag(zeros),"o", label="zeros")
plt.plot(np.real(poles), np.imag(poles),"x", label="poles")
plt.grid()
plt.axis("equal")
plt.legend()
plt.xlim([-2, 2])
plt.xlabel("Real Part")
plt.ylabel("Imag part")
Stabilité#
Définition#
un filtre est dit stable si sa réponse impulsionnelle est absolument sommable c-à-d
Propriété#
Un filtre est stable si tous les pôles de sa fonction de transfert sont inclus dans le cercle de rayon unité c-à-d si pour tout \(l=1,\cdots, L\)
Exemple#
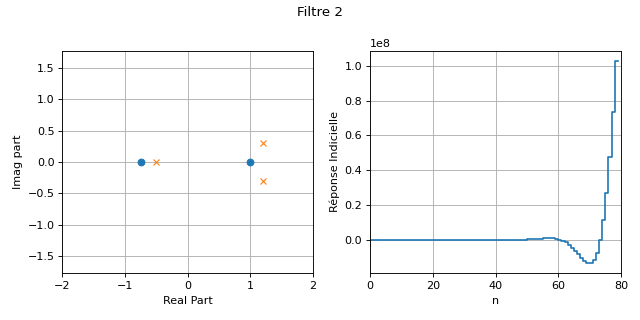
La figure suivante présente la localisation des pôles et des zéros ainsi que la réponse impulsionnelle de deux filtres IIR.
from scipy.signal import dlti
import matplotlib.pyplot as plt
# enter zero pole gain transfert function
H1 = dlti([1, -0.75], [-0.5, 0.2+0.3j, 0.2-0.3j], 5)
H2 = dlti([1, -0.75], [-0.5, 1.2+0.3j, 1.2-0.3j], 5)
H_list = [H1, H2]
for index, H in enumerate(H_list):
fig = plt.figure(figsize=(8,4))
# affichage des poles et zeros
ax1 = plt.subplot(1, 2, 1)
ax1.plot(np.real(H.zeros), np.imag(H.zeros),"o")
ax1.plot(np.real(H.poles), np.imag(H.poles),"x")
ax1.grid()
ax1.axis("equal")
ax1.set_xlim([-2, 2])
ax1.set_xlabel("Real Part")
ax1.set_ylabel("Imag part")
# affichage de la reponse impulsionnelle
n, y = H.impulse(n=80)
ax2 = plt.subplot(1, 2, 2)
ax2.step(n, np.squeeze(y))
ax2.grid()
ax2.set_xlim([0, 80])
ax2.set_xlabel("n")
ax2.set_ylabel("Réponse Indicielle")
fig.suptitle("Filtre {}".format(index+1))
plt.tight_layout()
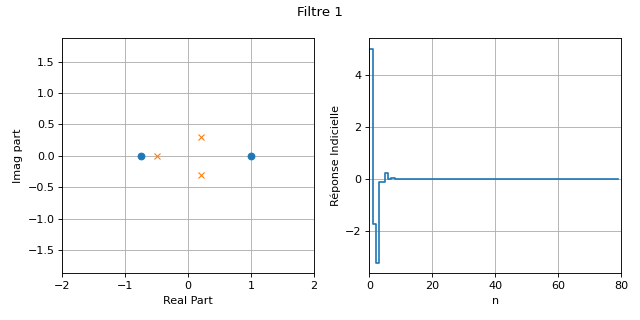
Le premier filtre est stable car tous ses pôles sont inclus dans le cercle de rayon unité.
Le second filtre est instable car il possède deux pôles pour lesquels le module est supérieur à 1. Pour ce second filtre, nous constatons que la réponse impulsionnelle semble tendre vers des valeurs infinies ( \(10^8\) !)
Analyse Fréquentielle#
Transformée de Fourier discrète#
Définition#
Une suite numérique \(x[n]\) peut se décomposer sous la forme
la quantité \(X(e^{j\omega})\) correspond à la transformée de Fourier (à temps discret) de \(x[n]\). La transformée de Fourier est définie par
Propriétés#
La transformée de Fourier d’un signal s’obtient en évaluant sa transformée en Z sur le cercle de rayon unité c-à-d \(z=e^{j\omega}\).
Comme \(X(e^{j\omega})=X(e^{j(\omega+2k\pi)})\) (\(k \in \mathbb{Z}\)), la transformée de Fourier à temps discret est \(2\pi\)-périodique. De plus lorsque \(x[n]\in \mathbb{R}\), il est possible de démontrer que \(X(e^{j\omega})=X^{*}(e^{-j\omega})`\) (symétrie hermitienne). Pour ces deux raisons, la transformée de Fourier est couramment représentée dans l’intervalle \([0,\pi]\).
La transformée de Fourier du signal de sortie d’un filtre LTI s’obtient en multipliant la transformée de Fourier de la réponse impulsionnelle du filtre par la transformée de Fourier de l’entrée c-à-d \(Y(e^{j\omega})=H(e^{j\omega})X(e^{j\omega})\). La transformée de Fourier de la réponse impulsionnelle est appelée réponse fréquentielle du filtre.
Réponse Fréquentielle#
Définition#
La réponse fréquentielle d’un filtre correspond à la transformée de Fourier de sa réponse impulsionnelle :
Représentation#
La réponse frequentielle \(H(e^{j\omega})\) est généralement une quantité complexe qu’il est possible de décomposer sous la forme
\(|H(e^{j\omega})|\) désigne le module de la réponse fréquentielle,
\(Arg[H(e^{j\omega})]\) désigne l’argument de la réponse fréquentielle.
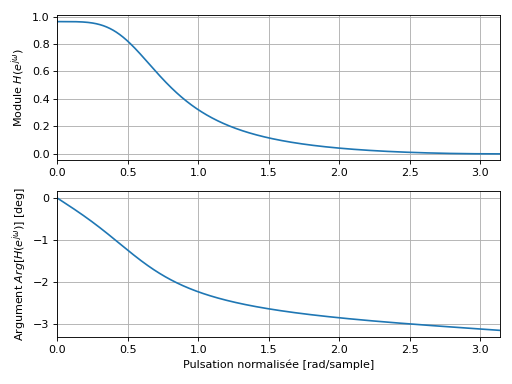
L’affichage du module et de l’argument permet d’avoir une interprétation concrète de l’effet du filtre sur une entrée quelconque. En effet à la pulsation \(\omega\), le filtre va appliquer un gain \(|H(e^{j\omega})|\) et un déphasage (retard) \(Arg[H(e^{j\omega})]\).
A titre d’illustration, la figure suivante présente le module et l’argument de la réponse fréquentielle d’un filtre.
from scipy.signal import dlti
import matplotlib.pyplot as plt
num = [0.065, 0.13, 0.065]
den = [1, -1.143, 0.413]
H = dlti(num, den)
w, Hjw = H.freqresp()
# affichage du module
ax1 = plt.subplot(2, 1, 1)
plt.plot(w, np.abs(Hjw))
plt.ylabel("Module $H(e^{j\omega})$")
plt.grid()
plt.xlim([0, np.pi])
ax1 = plt.subplot(2, 1, 2)
plt.plot(w, np.angle(Hjw))
plt.xlabel("Pulsation normalisée [rad/sample]")
plt.ylabel("Argument $Arg[H(e^{j\omega})]$ [deg]")
plt.grid()
plt.xlim([0, np.pi])
plt.tight_layout()
Lien avec l’équation de récurrence#
Pour les filtres décrits par une équation de récurrence, la réponse fréquentielle peut s’exprimer en fonction de la transformée de Fourier des coefficients \(a_l\) et \(b_m\) du filtre. Spécifiquement, nous obtenons :