Synthèse d’une sinusoïde#

Ce tutorial montre comment synthétiser un signal numérique contenant une sinusoïde de fréquence \(f_0\).

Avant Propos#

Modèles Mathématiques#

Signal à temps continu#

Pour rappel, une sinusoïde peut être modélisée par la fonction mathématique suivante :

\[x(t) = a \sin(2\pi f_0 t + \varphi)\]

  • \(f_0\): fréquence [Hz],

  • \(a\): amplitude crête,

  • \(\varphi\): phase initiale.

Comme \(t\in \mathbb{R}\), le signal \(x(t)\) est un signal à temps continu.

Signal à temps discret#

Pour numériser à temps continu, la technique la plus utilisée consiste à prélever, les valeurs du signal \(x(t)\) périodiquement. Ce processus est appelée échantillonnage. En échantillonnant le signal avec une période d’échantillonnage \(T_e\), le signal numérique s’exprime sous la forme :

\[x[n] = \left.x(t)\right|_{t=nT_e} = a \sin(2\pi f_0 n/F_e + \varphi)\]

  • \(x(t)\): signal à temps continu (\(t\in \mathbb{R}\)),

  • \(x[n]\): signal à temps discret (\(n\in \mathbb{N}\)),

  • \(T_e\): période d’échantillonnage [s],

  • \(F_e=1/T_e\): fréquence d’échantillonnage [Hz].

Note

Pour des signaux ayant des fréquences relativement élevées, on préfère souvent spécifier la fréquence d’échantillonnage [Hz] au lieu de la période d’échantillonnage [s].

Fréquence d’échantillonnage#

La fréquence échantillonnage est un paramètre critique lors de l’étape de numérisation. Le choix de la fréquence d’échantillonnage nécessite de faire un compromis entre la “fidélité” de la numérisation et la taille du signal dans l’espace mémoire.

  • Si \(F_e\) est trop faible (et donc \(T_e\) trop grand), le signal numérique risque d’être trop “approximatif”,

  • Si \(F_e\) est trop grand (et donc \(T_e\) trop petit), le signal numérique risque d’occuper un espace en mémoire inutilement important.

Pour fixer \(F_e\), la solution la plus utilisée consiste à se baser sur le théorème de Shannon. Ce théorème fixe une fréquence d’échantillonnage limite à partir de laquelle il est possible de reconstruire (restituer) parfaitement le signal à temps continu à partir du signal à temps discret. Pour obtenir une restitution parfaite, la fréquence d’échantillonnage doit respecter la condition de Shannon :

\[F_e \ge 2 f_{max}\]

  • \(F_e\): fréquence d’échantillonnage [Hz],

  • \(f_{max}\): fréquence maximale “restituable”.

A titre d’exemple, notre système auditif permet d’entendre des signaux sonores dans la bande fréquentielle \([0, 20]\) kHz. Pour cette raison, le format CD (premier format audionumérique grand public) utilise une fréquence d’échantillonnage :

\[F_e = 44100 \ge 2 \times 20000 Hz\]

Note

Lorsque la condition de Shannon n’est pas respectée, le signal restitué présente des artefacts de numérisation appelés repliement spectraux (aliasing).

Implémentation de Base#

Dans cette sous-section, nous proposons de synthétiser une sinusoïde de fréquence \(f_0\) en Python en utilisant uniquement la fonction sin et la constante pi de la librairie math.

L’implémentation repose sur la stratégie suivante.

  • Pour stocker la sinusoïde, nous utilisons une liste contenant N échantillons. Cette liste est pré-alloué en mémoire pour optimiser le temps d’execution du script.

  • Les N échantillons \(x[n]\) (avec \(n=0,\cdots,N-1\)) sont calculés les uns après les autres en utilisant une boucle for.

from math import sin, pi

# parametres du modele
N = 100
Fe = 44100
f0, a, varphi = 1000, 1, 0

# preallocation de l'espace memoire
x = [0]*N

for n in range(N):
    t = n/Fe
    x[n] = a * sin(2*pi*f0*t + varphi)

Implémentation Numpy#

Dans cette sous-section, nous proposons de synthétiser une sinusoïde de fréquence \(f_0\) en Python en utilisant la librairie numpy.

La librairie numpy propose des fonctionnalités permettant de gérer facilement des tableaux, vecteurs et matrice. Généralement, la librairie numpy permet de s’affranchir de l’utilisation de boucles pour la génération de signaux numériques.

import matplotlib.pyplot as plt  # pour affichage
import numpy as np

# parametres du modele
N = 100
Fe = 44100
f0, a, varphi = 1000, 1, 0

# utilisation de numpy
n_vect = np.arange(N)   # generation du tableau numpy contenant la base temps
x = a * np.sin(2*pi*f0*(n_vect/Fe) + varphi)

# affichage de la sinusoide
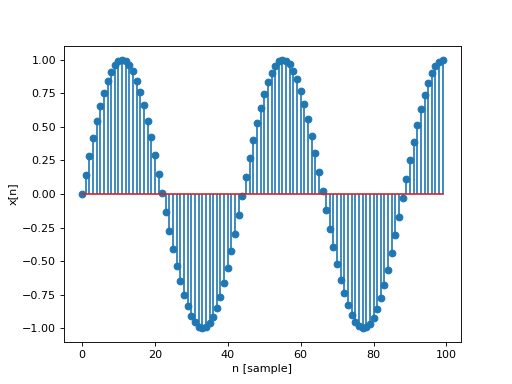
plt.stem(x)
plt.xlabel("n [sample]")
plt.ylabel("x[n]")
../_images/sine_wave-2.png