Synthèse d’un Filtre Numérique

Ce tutorial montre comment implémenter un filtre numérique en C. Pour obtenir les coefficients du filtre, nous allons utiliser dans un premier temps Python et les fonctionnalité de Scipy.

Cahier des charges

Le cahier des charges du filtre est spécifié ci-dessous :

• Fréquence de coupure: 4 kHz,

• Fréquence d’échantillonnage: 44.1 kHz,

• Type: Passe-bas,

• Ordre: 4.

Synthèse de filtre

Dans ce tutorial, nous allons utiliser la technique de synthèse de Butterworth. Cette technique de synthèse permet d’obtenir une réponse plate dans la bande passante. Notons toutefois que Scipy permet d’implementer facilement d’autres techniques de synthèse de filtres (voir documentation ).

• Fonction butter : https://docs.scipy.org/doc/scipy/reference/generated/scipy.signal.butter.html

from scipy import signal
import matplotlib.pyplot as plt

Fe = 44100
b, a = signal.butter(4, 4000, fs=Fe)

# affichage de la reponse frequentielle
w, h = signal.freqz(b, a, fs=Fe)
plt.semilogx(w, 20 * np.log10(abs(h)))
plt.xlabel('Frequence [Hz]')
plt.ylabel('Amplitude [dB]')
plt.axvline(4000, color='green')
plt.axhline(-3, color='green')
plt.ylim([-60, 10])
plt.grid()

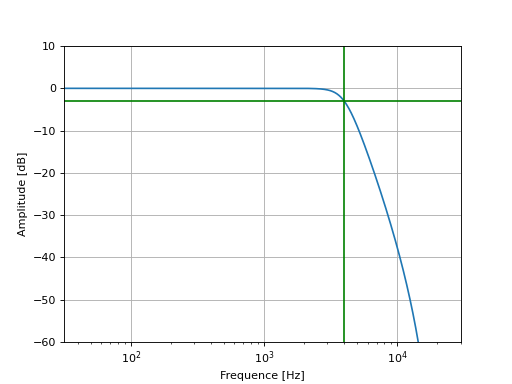
En utilisant la fonction butter, nous obtenons les coefficients du filtres ci-dessous :

b = [0.00345416, 0.01381663, 0.02072494, 0.01381663, 0.00345416]
a = [1., -2.5194645 ,  2.56083711, -1.20623537,  0.22012927]

Simulation

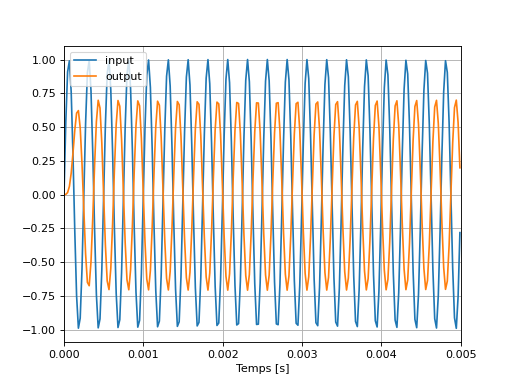
Pour vérifier le bon comportement du filtre, le script suivant montre l’allure de la sortie lorsqu’une sinusoïde de 4kHz est envoyé en entrée du filtre. Nous observons bien une réduction de l’amplitude de -3dB lorsque la fréquence est égale à la fréquence de coupure du filtre.

from scipy.signal import lfilter
import numpy as np
import matplotlib.pyplot as plt

Fe = 44100

# generation du signal d'entrée
t = np.arange(0, 0.005, 1/Fe)
x = np.sin(2*np.pi*4000*t)

# filtrage
b = [0.00345416, 0.01381663, 0.02072494, 0.01381663, 0.00345416]
a = [1., -2.5194645 ,  2.56083711, -1.20623537,  0.22012927]
y = lfilter(b, a, x)

# affichage de la sortie du filtre
plt.plot(t, x, label="input")
plt.plot(t, y, label="output")
plt.xlabel('Temps [s]')
plt.xlim([0, 0.005])
plt.grid()
plt.legend()

Implémentation C

Le code suivant montre comment implémenter le filtre en langage C.

/*
* Function: iir_filter
* --------------------
*   Apply a filter
*
*   input: the buffer with input samples
*   output: the output buffer
*   states; an array containing the filter state (previous inputs and outputs)
*/

void
iir_filter(const double *input,
          double *output,
          double *states,
          int N)
{
    double coef_b[5]= {0.00345416, 0.01381663, 0.02072494, 0.01381663, 0.00345416};
    double coef_a[5]= {1., -2.5194645 ,  2.56083711, -1.20623537,  0.22012927};

    for(int n=0; n<N; n++)
    {
        //compute filter output
        output[n] = coef_b[0]*input[n]
                  + coef_b[1]*states[0]
                  + coef_b[2]*states[1]
                  + coef_b[3]*states[2]
                  + coef_b[4]*states[3]
                  - coef_a[1]*states[4]
                  - coef_a[2]*states[5]
                  - coef_a[3]*states[6]
                  - coef_a[4]*states[7];

        //update filter states
        for (int i=6; i>=0; i--)
            {
            states[i+1] = states[i];
            }
        states[0] = input[n];
        states[4] = output[n];
    }
}