Décomposition d’un signal carré

Dans ce tutorial, nous montrons comment décomposer un signal carré via la décomposition en série de Fourier.

Modèle de Signal

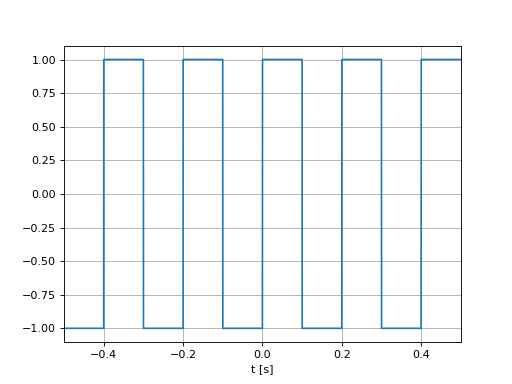
Sur la période \([-T_0/2, T_0/2]\), un signal carré est défini par

\[\begin{split}x(t) = \left\{\begin{array}{cc} -1 & \text{ si } -\frac{T_0}{2}\le t < 0\\ 1 & \text{ si } 0 \le t < \frac{T_0}{2}\\ \end{array}\right.\end{split}\]

import numpy as np
from scipy.signal import square
import matplotlib.pyplot as plt

t = np.arange(-0.5,0.5,0.0001)
f0 = 5
x = square(2*np.pi*f0*t)
plt.plot(t, x)
plt.grid()
plt.xlabel("t [s]")
plt.xlim([-0.5, 0.5])

Décomposition

• Pour \(n= 0\), le coefficient est donné par (le signal possède une moyenne nulle):

\[c_0=0\]

• Pour \(n\ne 0\), les coefficients de la décomposition en série de Fourier sont donnés par

\[\begin{split}c_n &= \frac{1}{T_0}\int_{[T_0]} x(t) e^{-2j\pi \frac{n}{T_0}t}dt\\ &= \frac{1}{T_0}\left(-\int_{-T_0/2}^0 e^{-2j\pi \frac{n}{T_0}t}dt+\int_0^{T_0/2} e^{-2j\pi \frac{n}{T_0}t}dt\right)\\ &= -\frac{1}{2j\pi n}\left(- \left[e^{-2j\pi \frac{n}{T_0}t}\right]_{-T_0/2}^0+\left[ e^{-2j\pi \frac{n}{T_0}t} \right]_0^{T_0/2} \right)\\ &= -\frac{1}{2j\pi n}\left( e^{j\pi n} + e^{-j\pi n} -2 \right)\\ &= \frac{1}{j\pi n}\left(1-\cos(\pi n)\right)\end{split}\]

Nous en déduisons que :

\[\begin{split}c_n = \left\{ \begin{array}{cc} \frac{2}{j\pi n}&\text{si n est impair}\\ 0&\text{sinon}\\ \end{array}\right.\end{split}\]

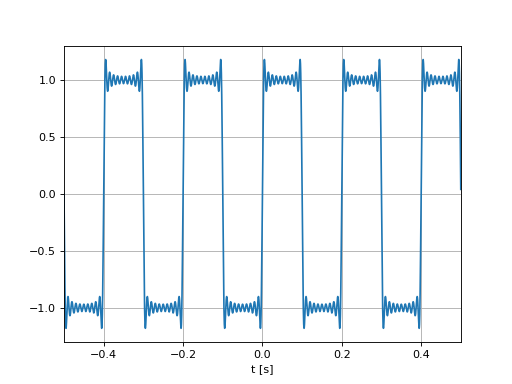
Reconstruction

class Fourier_Synth():

    def __init__(self, f0, L):
        self.f0 = f0
        self.L = L

    def get_c(self, n):
        if (n%2) == 0:
            c_n = 0
        else:
            c_n = 2/(1j*np.pi*n)
        return c_n

    def __call__(self, t):
        L = self.L
        x = np.zeros(len(t),dtype=complex)
        for n in range(-L, L+1):
            cn = self.get_c(n)
            x += cn*np.exp(2j*np.pi*n*self.f0*t)
        return x

# main program
t = np.arange(-0.5,0.5,0.0001)
waveform = Fourier_Synth(5, 20)
x = waveform(t)
plt.plot(t,x)
plt.grid()
plt.xlabel("t [s]")
plt.xlim([-0.5, 0.5])