Transformée de Fourier d’une Porte#

Dans ce tutorial, nous allons calculer puis analyser la transformée d’un signal porte de largeur L.

Modèle de Signal#

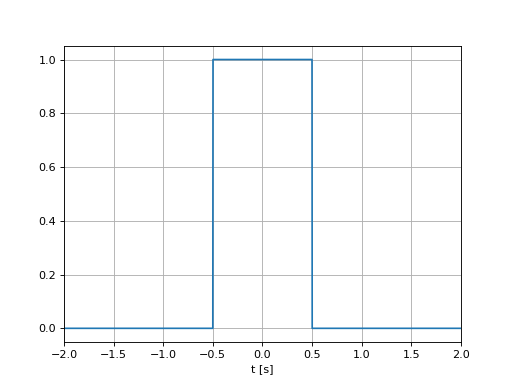
Le signal porte est défini par la relation :

\[\begin{split}\Pi_L(t)=\left\{\begin{array}{cc}1 &\text{si }|t| <\frac{L}{2}\\0 &\text{ailleurs}\end{array}\right.\end{split}\]
import numpy as np
import matplotlib.pyplot as plt

t = np.arange(-2,2,0.001)
L = 1
p = (np.abs(t)< (L/2))

plt.plot(t,p)
plt.grid()
plt.xlabel("t [s]")
plt.xlim([-2, 2])
../_images/fourier_transform_rect-1.png

Transformée de Fourier#

La transformée de Fourier du signal porte est égale à :

\[\begin{split}X(f) &= \mathcal{F}\left[x(t)\right]=\int_{-\infty}^{\infty} x(t) e^{-2j\pi ft}dt\\ &=\int_{-\frac{L}{2}}^{\frac{L}{2}} e^{-2j\pi ft}dt\\ &=\frac{1}{-2j\pi f} \left[e^{-2j\pi ft}\right]_{-\frac{L}{2}}^{\frac{L}{2}} \\ &=\frac{1}{2j\pi f} \left(e^{j\pi fL}-e^{-j\pi fL}\right)\\ &=\frac{1}{\pi f} \sin(\pi fL)\end{split}\]

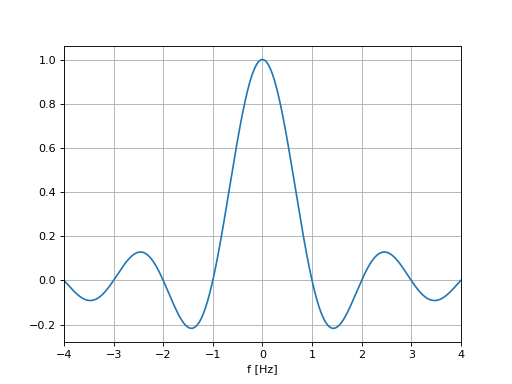
Cette fonction correspond à un sinus cardinal \(sinc(x)=sin(x)/x\) pondéré.

\[X(f) =L \text{sinc}(\pi fL)\]

Propriétés de la TF#

import numpy as np
import matplotlib.pyplot as plt

f = np.arange(-4, 4, 0.001)
L=1
X = L*np.sinc(f*L)

plt.plot(f, X)
plt.grid()
plt.xlabel("f [Hz]")
plt.xlim([-4, 4])
../_images/fourier_transform_rect-2.png

  • La fonction sinc de Scipy est définie par \(sinc(x)=sin(\pi x)/(\pi x)\) (voir documentation )

Valeur à l’origine#

La valeur à l’origine s’obtient en utilisant le fait que \(sinc(0)=1\). Nous obtenons alors

\[X(0) = L\]

Localisation des zéros#

La localisation des zéros sont donnés par \(\frac{1}{\pi f} \sin(\pi fL) = 0\). Il en vient que les fréquences \(f\) sont données par les zéros de la fonction (\(f\ne 0\))

\[\sin(\pi fL) = 0 \Rightarrow \pi fL = k\pi (k\in \mathbb{Z}^+)\]

Finalement, nous obtenons :

\[f = \frac{k}{L} \text{ pour } k\in \mathbb{Z}^+\]