Analyse Spectrale

Ce tutorial montre comment effectué une analyse spectrale d’un signal.

Modèle de Signal

Afin d’illustrer ce tutorial, nous allons utiliser le signal suivant

\[x(t) = a_1 \cos(2\pi f_1 t) + a_2 \cos(2\pi f_2 t) + b(t)\]

• \(b(t) \sim \mathcal{N}(0,\frac{\sigma^2}{2})\) est un bruit additif Gaussien de moyenne nulle et de variance \(\sigma^2\).

Le code suivant montre comment générer une réalisation du signal \(x(t)\) échantillonné à la fréquence d’échantillonnage \(F_e\).

import numpy as np
from numpy.fft import fft, fftshift, fftfreq
import matplotlib.pyplot as plt

def model(t, f1, a1=1, f2=0, a2=0, sigma2=0):
    N = len(t)
    s1 = a1*np.cos(2*np.pi*f1*t)
    s2 = a2*np.cos(2*np.pi*f2*t)
    b = np.sqrt(sigma2)*np.random.randn(N)
    x = s1 + s2 +b
    return x

Fs = 1000
f1 = 10
t =  np.arange(1000)/Fs
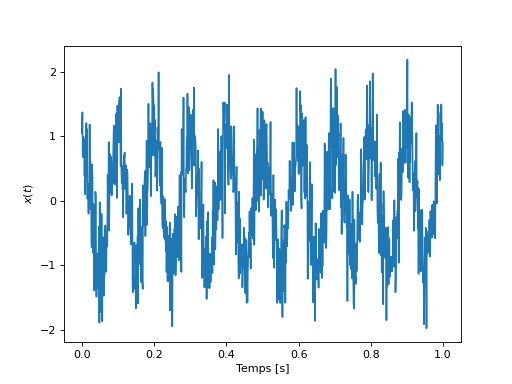
x = model(t, f1, sigma2=0.2)

plt.plot(t, x)
plt.xlabel("Temps [s]")
plt.ylabel("$x(t)$")

FFT

Numpy intègre des fonctionnalités pour l’évaluation rapide de la DFT.

Note

• https://numpy.org/doc/stable/reference/generated/numpy.fft.fft.html

• https://numpy.org/doc/stable/reference/generated/numpy.fft.fftfreq.html

• https://numpy.org/doc/stable/reference/generated/numpy.fft.fftshift.html

# parameter
NFFT = 2**13

# evaluate the FFT of x and shift the zero-frequency component to the center of the spectrum.
N = len(x)
fftx = (1/N)*fft(x, NFFT)
X = fftshift(fftx)
f = fftshift(fftfreq(NFFT, d=1/Fs))

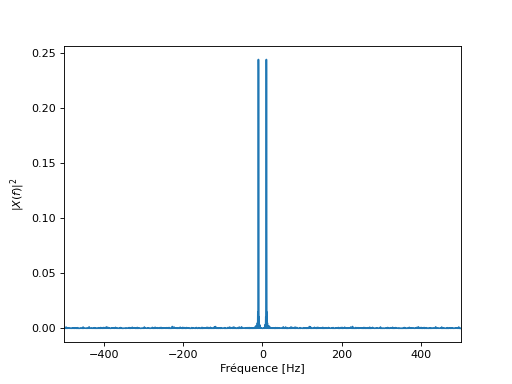
Echelle Linéaire

plt.plot(f, abs(X)**2)
plt.xlim([-Fs/2, Fs/2])
plt.xlabel("Fréquence [Hz]")
plt.ylabel("$|X(f)|^2$")

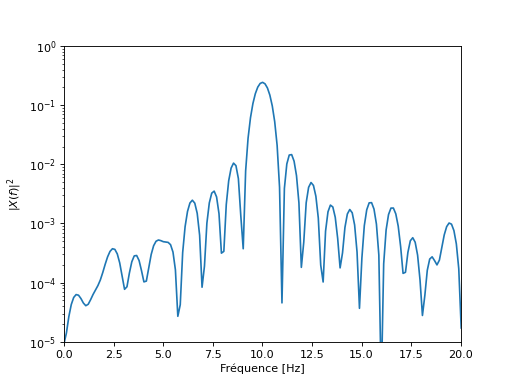
Echelle Semi-Log

plt.semilogy(f, abs(X)**2)
plt.xlim([0, 20])
plt.ylim([10**-5, 1])
plt.xlabel("Fréquence [Hz]")
plt.ylabel("$|X(f)|^2$")

Périodogramme

La fonction periodogram de scipy permet d’obtenir rapidement le periodogramme d’un signal.

from scipy.signal import periodogram, get_window

f, Pxx_den = periodogram(x, Fs, nfft=NFFT, scaling="spectrum")

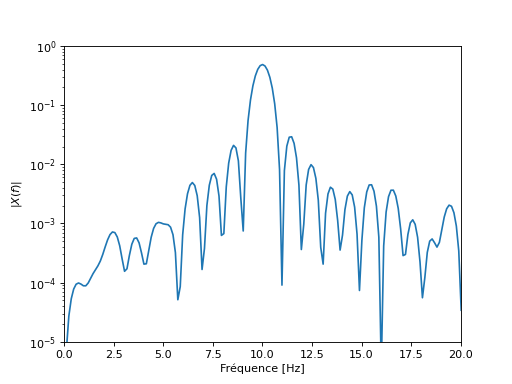
plt.semilogy(f, Pxx_den)
plt.xlim([0, 20])
plt.ylim([10**-5, 1])
plt.xlabel("Fréquence [Hz]")
plt.ylabel("$|X(f)|$")

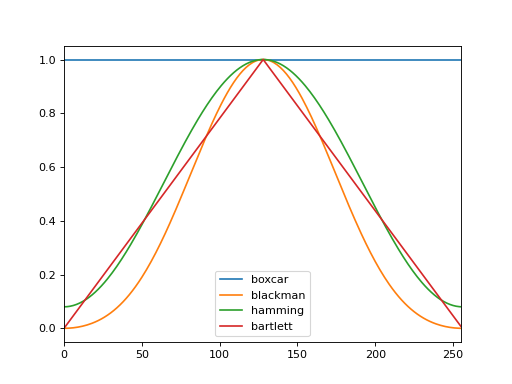
Liste des fenêtres

Representation Temporelle

Nx = 256
window_name_list = ["boxcar", "blackman", "hamming", "bartlett"]
for window_name in window_name_list:
    w = get_window(window_name, Nx)
    plt.plot(w, label=window_name)

plt.legend()
plt.xlim([0, Nx-1])