MIMO Chain Tutorial#

This tutorial demonstrates how to simulate a basic MIMO (Multiple-Input Multiple-Output) communication system using the comnumpy library. You will learn how to:

  • Build a MIMO simulation chain with Rayleigh fading.

  • Visualize received and equalized signals.

  • Compare detection algorithms (ZF, MMSE, OSIC, ML).

  • Perform a Monte Carlo evaluation of Symbol Error Rate (SER).

This tutorial is ideal for engineers or students learning about MIMO systems, and offers both practical insights and theoretical understanding.

Prerequisites#

Ensure you have the following Python libraries installed:

  • numpy

  • matplotlib

  • comnumpy

  • tqdm

Simulation Setup#

1. Import Libraries#

We start by importing the required Python libraries and comnumpy components:

import numpy as np
import numpy.linalg as linalg
import matplotlib.pyplot as plt

from tqdm import tqdm
from comnumpy.core import Sequential, Recorder
from comnumpy.core.generators import SymbolGenerator
from comnumpy.core.mappers import SymbolMapper
from comnumpy.core.metrics import compute_ser, compute_ber
from comnumpy.core.utils import get_alphabet
from comnumpy.mimo.channels import FlatMIMOChannel, AWGN
from comnumpy.mimo.utils import rayleigh_channel
from comnumpy.mimo.detectors import MaximumLikelihoodDetector, LinearDetector, OrderedSuccessiveInterferenceCancellationDetector

2. Define System Parameters#

We define the number of transmit/receive antennas, the modulation order (PSK), and the noise variance:


# Parameters
N = 1000
N_r, N_t = 3, 2
M = 4
alphabet = get_alphabet("PSK", M)
M = len(alphabet)
sigma2 = 0.1
H = rayleigh_channel(N_r, N_t)

The modulation alphabet is automatically generated from the given parameters.

3. Build the MIMO Chain#

We create a transmission chain consisting of a symbol generator, symbol mapper, and Rayleigh fading channel:

# construct chain
chain = Sequential([SymbolGenerator(M),
                    Recorder(name="data_tx"),
                    SymbolMapper(alphabet),
                    FlatMIMOChannel(H, name="channel"),
                    AWGN(sigma2, name="noise")
                    ])
Y = chain((N_t, N))

This simulates a MIMO transmission over a flat-fading channel with additive Gaussian noise. The received signal can be described by :

\[\mathbf{y}[n] = \mathbf{H}\mathbf{x}[n] + \mathbf{b}[n]\]

Visualize the Received Signal#

Let’s inspect the received signal on each receive antenna:

# extract signals
S_tx = chain["data_tx"].get_data()

# Figure 1: received signal
fig1, axes1 = plt.subplots(nrows=1, ncols=N_r, figsize=(4 * N_r, 4))
for num_channel in range(N_r):
    y = Y[num_channel, :]
    ax = axes1[num_channel]
    ax.plot(np.real(y), np.imag(y), ".")
    ax.set_title(f"Received signal (antenna {num_channel+1})")
    ax.set_aspect("equal", adjustable="box")
    ax.set_xlim([-2, 2])
    ax.set_ylim([-2, 2])
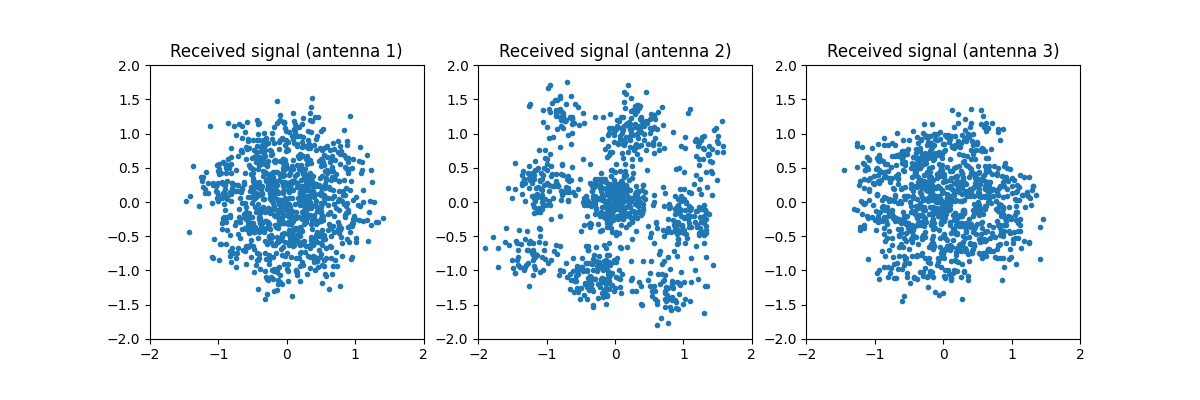
../_images/monte_carlo_mimo_fig1.png

You should observe that the received signal consists of noisy superpositions of multiple transmitted streams.

5. Zero-Forcing Equalization#

We now apply Zero-Forcing (ZF) equalization using the pseudo-inverse of the channel matrix:

# ZF equalization
H_inv = linalg.pinv(H)
X_est = np.matmul(H_inv, Y)

This separates the transmitted streams assuming ideal channel knowledge and no noise contribution. The ZF equalized symbol are given by

\[\mathbf{z}[n] = \mathbf{H}^{\dagger}\mathbf{y}[n]\]

Visualize the Estimated Symbols#

We plot the ZF-equalized symbols:


# Figure 2: estimated signal
fig2, axes2 = plt.subplots(nrows=1, ncols=N_t, figsize=(4 * N_t, 4))
for num_channel in range(N_t):
    x_est = X_est[num_channel, :]
    ax = axes2[num_channel]
    ax.plot(np.real(x_est), np.imag(x_est), ".")
    ax.set_title(f"Estimated signal (antenna {num_channel+1})")
    ax.set_aspect("equal", adjustable="box")
    ax.set_xlim([-2, 2])
    ax.set_ylim([-2, 2])
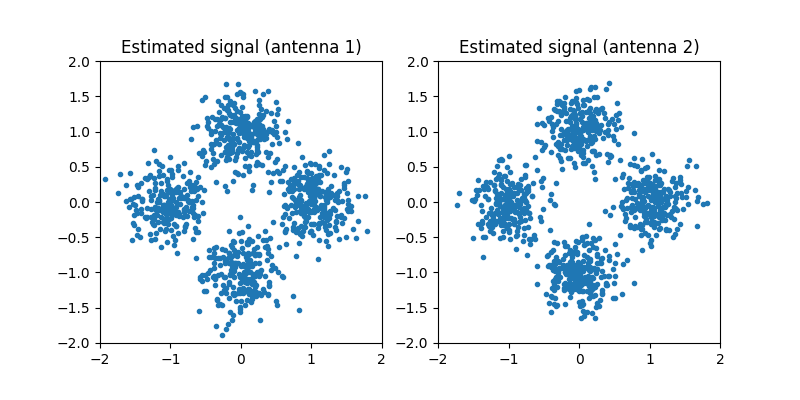
../_images/monte_carlo_mimo_fig2.png

The estimated points should cluster near the ideal constellation points, although some noise remains.

7. Compare Detection Algorithms#

We now compare four MIMO detection strategies:

  • ML: Maximum Likelihood

\[\widehat{\mathbf{x}}_{ML}[n] = \arg \min_{\mathbf{x}\in \mathcal{M}^{N_t}}\|\mathbf{y}[n] - \mathbf{H}\mathbf{x}\|^2_2\]

  • ZF: Zero-Forcing

\[\begin{split}\widehat{\mathbf{x}}_{ZF}[n] &= \boldsymbol \Pi_{\mathcal{M}}(\mathbf{z}[n])\\ \mathbf{z}[n] &= \mathbf{H}^{\dagger}\mathbf{y}[n]\end{split}\]

  • MMSE: Minimum Mean Square Error

\[\begin{split}\widehat{\mathbf{x}}_{MMSE}[n] &= \boldsymbol \Pi_{\mathcal{M}}(\mathbf{z}[n])\\ \mathbf{z}[n] &= \left(\left(\mathbf{H}^H\mathbf{H}\right)^{-1}+\sigma^2 \mathbf{I}_{N_t}\right)\mathbf{H}^H\mathbf{y}[n]\end{split}\]

  • OSIC: Ordered Successive Interference Cancellation

These detectors are directly implemented in comnumpy.


# evaluate the BER for several detectors
detector_list = [
    LinearDetector(alphabet, H, method="zf", name="ZF"),
    LinearDetector(alphabet, H, sigma2=sigma2, method="mmse", name="MMSE"),
    OrderedSuccessiveInterferenceCancellationDetector(alphabet, "sinr", H, sigma2=sigma2, name="OSIC"),
    MaximumLikelihoodDetector(alphabet, H, name="ML")
    ]
for detector in detector_list:
    S_est = detector(Y)
    ser = compute_ser(S_tx, S_est)
    name = detector.name
    print(f"* detector {name}: ser={ser}")

Each detector is tested on the same channel realization, and the Symbol Error Rate (SER) is printed. We obtain the following outputs:

  • detector ZF: ser=0.005

  • detector MMSE: ser=0.004

  • detector OSIC: ser=0.001

  • detector ML: ser=0.0005

8. Monte Carlo Evaluation#

To get a more reliable estimate of the SER, we run a Monte Carlo simulation.

# perform monte carlo simulation
snr_dB_list = np.arange(0, 20, 2)
N_test = 1000
ser_data = np.zeros((len(snr_dB_list), len(detector_list)))

for index_snr, snr_dB in enumerate(tqdm(snr_dB_list)):
    sigma2 = N_t * (10**(-snr_dB/10))
    chain["noise"].value = sigma2

    # update sigma2 for the MMSE and OSIC detector
    detector_list[1].sigma2 = sigma2
    detector_list[2].sigma2 = sigma2

    for trial in range(N_test):
   
        # new channel realization
        H = rayleigh_channel(N_r, N_t)
        chain["channel"].H = H

        # generate data
        Y = chain((N_t, N))
        S_tx = chain["data_tx"].get_data()

        # test detector
        for index, detector in enumerate(detector_list):

            # update channel information
            detector.H = H
            # perform detection
            S_est = detector(Y)
            # evaluate metrics
            ser_data[index_snr, index] += compute_ser(S_tx, S_est)

    ser_data[index_snr, :] /= N_test

This simulates multiple random channels and noise realizations for a range of SNR values.

9. Plot SER vs SNR#

Finally, we plot the SER for each detection scheme as a function of SNR:

# plot figures
plt.figure()
for index, detector in enumerate(detector_list):
    plt.semilogy(snr_dB_list, ser_data[:, index], label=detector.name)
plt.ylabel("SER")

plt.xlabel("SNR (dB)")
plt.xlim([0, 20])
plt.ylim([10**-3, 1])
plt.legend()
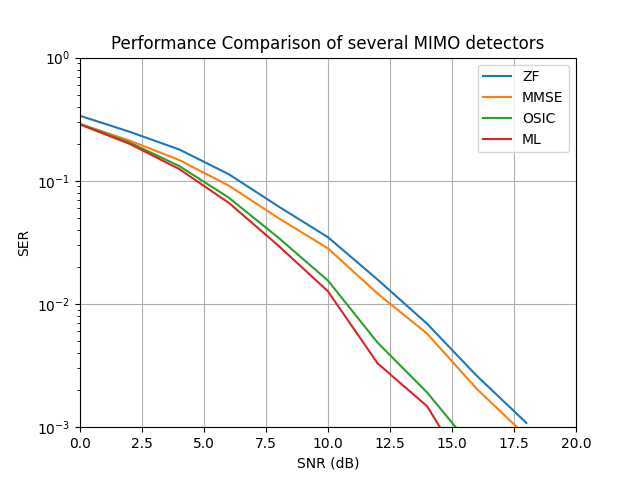
../_images/monte_carlo_mimo_fig3.png

This figure compares detection methods as a function of the signal-to-noise ratio (SNR). The maximum-likelihood (ML) detector delivers the best performance, albeit at higher computational cost. The OSIC detector performs close to ML.

Conclusion#

This tutorial highlighted:

  • How to simulate a MIMO transmission with comnumpy.

  • How ZF equalization recovers the signal from a multi-stream mixture.

  • How various MIMO detectors behave under different SNR conditions.

  • Why advanced detection schemes like OSIC and ML outperform linear methods in difficult channel conditions.

With comnumpy, you can rapidly prototype, test, and visualize MIMO systems — whether for research, teaching, or personal learning.