Fonction de Transfert en BF

Objectif

Dans ce tutorial, nous montrons comment utiliser l’expression de la FTBF pour régler un correcteur proportionnel.

Boucle Fermée

La fonction de transfert est égale à :

\[F(z) = \frac{0.022}{z-0.666}\]

La période d’échantillonnage est fixée à \(T_e=0.1\) s. L’objectif est de calibrer un correcteur proportionnel (c-a-d \(C(z)=K\)) de sorte à obtenir un gain statique en boucle fermée de 0.8

Méthodologie

Pour calibrer la valeur de \(K\), nous allons procéder en trois temps:

1. Calcul de la fonction de transfert en boucle fermée (FTBF),

2. Calcul du gain statique de la boucle fermée,

3. Calibration de K.

FTBF

Pour calculer la FTBF, nous allons utiliser la formule (à connaître):

\[FTBF(z) = \frac{A(z)}{1+A(z)B(z)}\]

• \(A(z)\): Fonction de transfert de la chaîne directe,

• \(B(z)\): Fonction de transfert de la chaîne de retour.

Dans notre problème, nous avons \(A(z)=K \times F(z)\) et \(B(z)=1\). La FTBF s’exprime alors sous la forme :

\[FTBF(z) = \frac{\frac{0.022K}{z-0.666}}{1+\frac{0.022K}{z-0.666}}\]

Après simplification, nous obtenons :

\[FTBF(z) = \frac{0.022K}{z-0.666+0.022K}\]

Gain statique

Comme le système est un système à temps discret, le gain statique \(G\) est donné par \(FTBF(1)\). Il en vient que

\[G = FTBF(1) = \frac{0.022K}{1-0.666+0.022K}= \frac{0.022K}{0.333+0.022K}\]

Calibration

Pour obtenir un gain statique de 0.8, il faut poser l’égalité:

\[\frac{0.022K}{0.333+0.022K} = 0.8\]

Nous obtenons :

\[\begin{split}0.022K &= 0.8 (0.333+0.022K)\\ 0.0044K &= 0.266\\ K & \approx 60\end{split}\]

Vérification

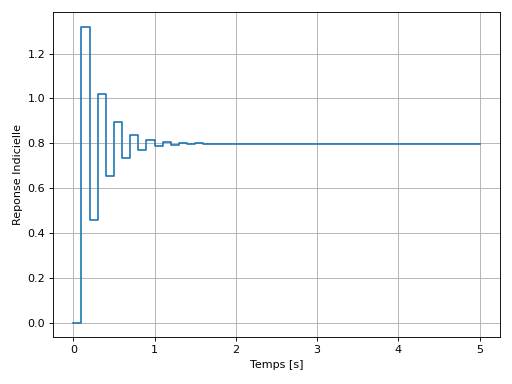
En asservissement, il est toujours utilise de vérifier le résultat avec une simulation. En utilisant Python, nous obtenons la réponse indicielle suivante.

from control import tf, feedback, step_response
import matplotlib.pyplot as plt

Te = 0.1
K = 60
Fz = tf([0.022], [1, -0.666], Te)
Az = K*Fz
FTBFz = feedback(Az, 1)
T, yout = step_response(FTBFz)

plt.step(T, yout, where="post")
plt.xlabel("Temps [s]")
plt.ylabel("Reponse Indicielle")
plt.grid()
plt.tight_layout()