Equation de récurrence#
Objectif#
Dans ce tutorial, nous montrons comment obtenir l’équation de récurrence d’un système à temps discret décrit par une fonction de transfert \(F(z)\). Pour illustrer ce tutoriel, nous allons considérer la fonction de transfert suivante :
Méthodologie#
Pour obtenir l’équation de récurrence, nous allons précéder en deux temps
Obtention d’une équation impliquant la transformée en Z de la sortie, \(S(z)\), et la transformée en Z de l’entrée, \(E(z)\).
Ecriture de l’équation en puissances de z négatives.
Passage à la transformée en Z inverse.
Transformée en Z#
En utilisant l’expression de \(F(z)\), nous obtenons :
Puissances de z négatives#
Pour obtenir une écriture en puissance de z négatives, nous allons multiplier les deux parties de l’égalité par \(z^{-1}\).
Transformée en Z inverse#
En utilisant la propriété de linéarité et du retard, nous obtenons :
Finalement, l’équation de récurrence est donnée par :
Vérification#
Pour vérifier notre équation, nous allons déterminer les premiers échantillons de sortie lorsque l’entrée est un échelon unitaire (\(e[n]=u[n]\)). Ces échantillons en sortie seront comparés avec ceux obtenus en utilisant Python.
Lorsque l’entrée est un échelon unitaire, les premiers échantillons sont donnés par :
En utilisant Python, nous obtenons la réponse indicielle suivante.
from control import tf, step_response
import matplotlib.pyplot as plt
Te = 1
Fz = tf([2], [4, 1], Te)
T, yout = step_response(Fz)
plt.step(T, yout, where="post")
plt.xlabel("Temps [s]")
plt.ylabel("Reponse Indicielle")
plt.grid()
plt.tight_layout()
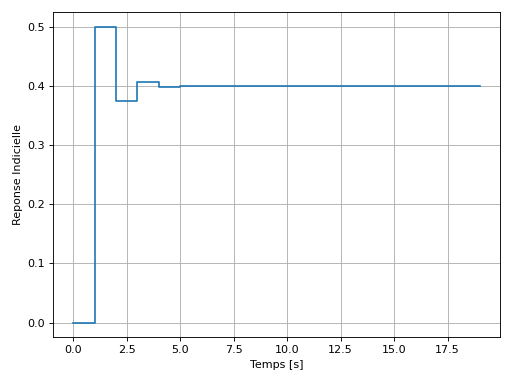
Nous pouvons constater que les deux réponses correspondent bien.