Python#

Introduction#

Dans ce cours nous allons utiliser Python pour l’analyse des filtres et plus généralement des systèmes LTI. L’utilisation de Python pour l’analyse des systèmes linéaires invariants dans le temps (LTI) offre plusieurs avantages.

  • Librairies puissantes :

    • NumPy : Une bibliothèque pour la manipulation d’arrays et matrices, essentielle pour les calculs liés aux systèmes LTI.

    • SciPy : Offre le module signal qui fournit des outils pour l’analyse et la conception de systèmes LTI, y compris des fonctions pour la transformation de Laplace, de Fourier, la convolution, etc.

    • matplotlib : Une bibliothèque de visualisation permettant de tracer des réponses en fréquence, des réponses impulsionnelles et temporelles, et d’autres aspects des systèmes LTI.

  • Flexibilité : Contrairement à des logiciels spécifiques qui peuvent être limités dans leurs fonctionnalités ou leur capacité d’extension, Python est un langage de programmation complet. Cela signifie que vous pouvez facilement automatiser des tâches, effectuer des analyses complexes, ou même intégrer l’analyse LTI dans des applications plus grandes.

  • Interopérabilité: Python peut être facilement intégré avec d’autres logiciels ou langages de programmation. Cela est particulièrement utile si vous devez, par exemple, combiner l’analyse LTI avec des simulations réalisées dans d’autres logiciels.

  • Open Source et Gratuit : Python et ses librairies sont open source, ce qui signifie qu’ils sont gratuits à utiliser et qu’ils bénéficient du support d’une large communauté. Vous pouvez les adapter selon vos besoins sans restriction.

  • Plateforme indépendante : Python est multiplateforme, ce qui signifie que vous pouvez exécuter vos scripts d’analyse LTI sur Windows, MacOS, Linux, et même sur certains systèmes embarqués.

import numpy as np
import matplotlib.pyplot as plt
from scipy.signal import lti, butter

Analyse de Systèmes#

Création d’un système#

\[H(p)=\frac{b_Np^N+\cdots+b_1p+b_0}{a_Np^N+\cdots+a_1p+a_0}\]
num = [1, 2, 3]   # coefficients rangés par puissance décroissante
den = [4, 5, 6]   # coefficients rangés par puissance décroissante
sys = lti(num, den)

Attention à l’ordre des coefficients, les puissances en p les plus grandes sont placées devant !

Poles and zeros#

Les pôles et zeros sont des attributs de l’objet lti.

# compute poles and zeros
poles = sys.poles
zeros = sys.zeros

# plot figure
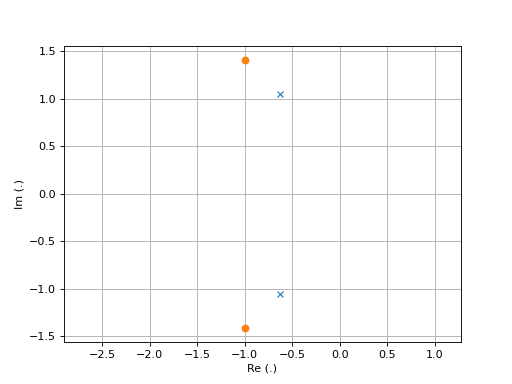
plt.plot(np.real(poles), np.imag(poles), 'x')
plt.plot(np.real(zeros), np.imag(zeros), 'o')
plt.axis("equal")
plt.xlabel("Re (.)")
plt.ylabel("Im (.)")
plt.grid()
../_images/python-3.png

Response Temporelle#

t,s = sys.step()

# plot figure
plt.plot(t,s)
plt.grid()
plt.xlabel("time [s]")
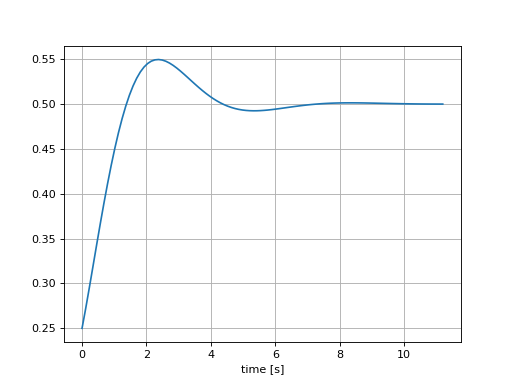
../_images/python-4.png

  • step response: sys.step()

  • impulse response: sys.impulse()

  • arbitrary response: sys.output()

Response Fréquentielle#

# compute frequency response
w,Hjw = sys.freqresp()
H_mod = np.abs(Hjw)
H_phase = 180*np.angle(Hjw)/np.pi     #convert radian to degree

# plot figure
plt.subplot(2,1,1)
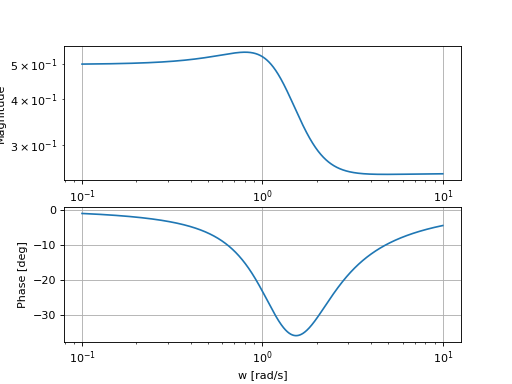
plt.loglog(w,H_mod)
plt.ylabel("Magnitude")
plt.grid()
plt.subplot(2,1,2)
plt.semilogx(w,H_phase)
plt.ylabel("Phase [deg]")
plt.xlabel("w [rad/s]")
plt.grid()
../_images/python-5.png

Analyse d’un signal#

Création d’un signal audio#

import numpy as np
import IPython.display as ipd

Fs = 22050 # sample rate
t = np.arange(0, 1, 1/Fs)
x = 0.5*np.sin(2*np.pi*440*t)
ipd.Audio(x, rate=Fs)

Chargement d’un signal audio#

from scipy.io import wavfile

Fs, data = wavfile.read("mon_fichier_audio.wav")

Affichage du spectre#

import matplotlib.pyplot as plt

...

plt.magnitude_spectrum(data, Fs=Fs)

Synthèse d’un filtre#

Butterworth#

N = 5       # ordre du filtre
wc = 1000   # pulsation de coupure (rad/s)

num, den = butter(N, wc, analog=True)
sys2 = lti(num, den)

Affichage du Prototype#

def plot_prototype(wc,Tc,ws,Ts):
    ax = plt.gca()
    xmin, xmax = ax.get_xlim()
    ymin, ymax = ax.get_ylim()
    options = {"fill": False,"closed": True,"color": 'b',"hatch": "/"}

    polygon_data1 = [[xmin,Tc], [wc,Tc], [wc,ymin], [xmin,ymin]]
    polygon_data2 = [[xmin,ymax], [xmin,1], [ws,1], [ws,Ts], [xmax,Ts], [xmax,ymax], [xmin,ymax]]
    patch1 = plt.Polygon(polygon_data1,**options)
    patch2 = plt.Polygon(polygon_data2,**options)
    ax.add_patch(patch1)
    ax.add_patch(patch2)

# compute frequency response
w,Hjw = sys2.freqresp()
H_mod = np.abs(Hjw)

# plot frequency response
plt.loglog(w,H_mod)
plt.ylabel("Magnitude")
plt.ylim([0.01,2])
plt.xlabel("w [rad/s]")
plot_prototype(wc,1/np.sqrt(2),2000,0.1);
../_images/python-7.png